题目内容
11.等差数列{an}的首项a1=1,其前n项和为Sn,且a3+a5=a4+7.(Ⅰ)求{an}的通项公式;
(Ⅱ)求满足不等式Sn<3an-2的n的值.
分析 (Ⅰ)利用等差数列{an}的通项公式求出公差d=2,由此能求出an.
(Ⅱ)由a1=1,an=2n-1,求出${S_n}=\frac{{{a_1}+{a_n}}}{2}n={n^2}$,由此能求出满足不等式Sn<3an-2的n的值.
解答 解:(Ⅰ)设数列{an}的公差为d.….(1分)
因为a3+a5=a4+7,所以2a1+6d=a1+3d+7.….(3分)
因为a1=1,所以3d=6,即d=2,….(5分)
所以an=a1+(n-1)d=2n-1.….(7分)
(Ⅱ)因为a1=1,an=2n-1,所以${S_n}=\frac{{{a_1}+{a_n}}}{2}n={n^2}$,….(9分)
所以n2<3(2n-1)-2,所以n2-6n+5<0,….(11分)
解得1<n<5,所以n的值为2,3,4.….(13分)
点评 本题考查数列的通项公式的求法,考查满足不等式的值的求法,是中档题,解题时要认真审题,注意等差数列性质的合理运用.

练习册系列答案
相关题目
2.函数y=$lo{g}_{\frac{1}{2}}sin(2πx+\frac{π}{4})$的单调递减区间是( )
| A. | [$-\frac{3}{8}$+k,$\frac{1}{8}$+k](k∈Z) | B. | (-$\frac{1}{8}$+k,$\frac{1}{8}$+k](k∈Z) | C. | [$-\frac{3}{8}$+k,$\frac{1}{8}$+k](k∈Z) | D. | [$\frac{1}{8}$+k,$\frac{3}{8}$+k)(k∈Z) |
16.一个三棱锥的三视图如图所示,则该三棱锥的体积为( )
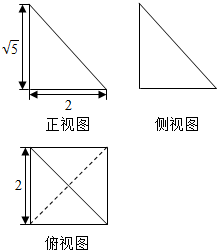

| A. | $\frac{2\sqrt{5}}{3}$ | B. | $\frac{4\sqrt{5}}{3}$ | C. | 4$\sqrt{5}$ | D. | 2$\sqrt{5}$ |
3.执行如图所示的程序框图,若输入的c的值为3,则输出的结果是( )


| A. | 27 | B. | 9 | C. | 8 | D. | 3 |
1.已知{an}是等差数列,{bn}是等比数列,bn>0恒成立,若a2=b2且a8=b8,则( )
| A. | a5≥b5 | B. | a5≤b5 | C. | a5>b5 | D. | a5<b5 |