题目内容
3.已知函数f(x)=$\frac{{x}^{2}+bx+a}{x}$(a∈R+).(1)若函数f(x)是奇函数,求b的值;
(2)在(1)的条件下求函数f(x)在x∈[2,±∞)上的值域.
分析 (1)利用函数是奇函数,建立方程,即可求出b;
(2)f(x)=x+$\frac{a}{x}$,分类讨论,结合基本不等式,函数的单调性,即可求出函数的值域.
解答 解:(1)∵函数f(x)是奇函数,
∴f(-1)=-f(1),
∴-(1-b+a)=-(1+b+a),
∴b=0;
(2)f(x)=x+$\frac{a}{x}$
a≥4时,f(x)=x+$\frac{a}{x}$≥2$\sqrt{a}$,值域为[2$\sqrt{a}$,+∞);
0<a<4时,f(x)=x+$\frac{a}{x}$≥f(2)=2+$\frac{a}{2}$,值域为[2+$\frac{a}{2}$,+∞).
点评 本题考查函数的奇偶性、值域,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
14.已知圆C的方程为(x-1)2+(y-1)2=4,过直线x-y-6=0上的一点M作圆C的切线,切点为N,则|MN|的最小值为( )
| A. | 2$\sqrt{3}$ | B. | $\sqrt{14}$ | C. | 4 | D. | 3$\sqrt{2}$ |
16.一个三棱锥的三视图如图所示,则该三棱锥的体积为( )
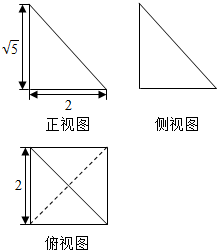

| A. | $\frac{2\sqrt{5}}{3}$ | B. | $\frac{4\sqrt{5}}{3}$ | C. | 4$\sqrt{5}$ | D. | 2$\sqrt{5}$ |
