题目内容
设函数f(x)=x-
,对任意x∈[1,+∞),f(mx)+mf(x)>0恒成立,则实数m的取值范围是( )
| 1 |
| x |
| A、(-∞,-1)∪(1,+∞) |
| B、(1,+∞) |
| C、(-∞,-1) |
| D、不能确定 |
考点:函数恒成立问题
专题:函数的性质及应用
分析:先将已知代入条件,将函数原式化简成2mx2>m+
恒成立,x>1时.然后讨论m的符号将m分离出来,然后研究函数的最值.
| 1 |
| m |
解答:
解:由f(mx)+mf(x)>0得mx-
+mx-
>0,对任意x∈[1,+∞)恒成立.
整理得2mx>(m+
)
恒成立,即2mx2>m+
恒成立.
显然m≠0,
①当m>0时,2x2>1+
,显然当x=1时y=2x2最小为2,即1+
<2,
解得m>1或m<-1.所以m>1符合题意.
②当m<0时,1+
>2x2,此时y=2x2无最大值,所以不成立.
综上,所求实数m的范围是m>1.
故选B.
| 1 |
| mx |
| m |
| x |
整理得2mx>(m+
| 1 |
| m |
| 1 |
| x |
| 1 |
| m |
显然m≠0,
①当m>0时,2x2>1+
| 1 |
| m2 |
| 1 |
| m2 |
解得m>1或m<-1.所以m>1符合题意.
②当m<0时,1+
| 1 |
| m2 |
综上,所求实数m的范围是m>1.
故选B.
点评:本题考查了不等式恒成立问题的思路,一般是转化为函数的最值问题求解,能分离参数的尽量分离参数.

练习册系列答案
相关题目
设集合A={1,3,4},B={2,3,6},则A∪B等于( )
| A、{3} |
| B、{1,2,3,4} |
| C、{1,2,3,6} |
| D、{1,2,3,4,6} |
 选修4-5不等式选讲
选修4-5不等式选讲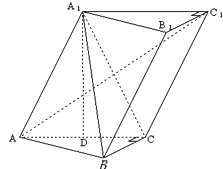 在三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=AA1=2,A1在底面ABC上的射影恰为AC的中点D.
在三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=AA1=2,A1在底面ABC上的射影恰为AC的中点D.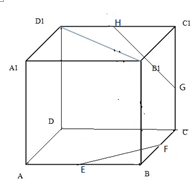 如图,E、F、G、H分别是正方体ABCD-A1B1C1D1的棱AB、BC、CC1、C1D1的中点.证明:FE、HG、DC三线共点.
如图,E、F、G、H分别是正方体ABCD-A1B1C1D1的棱AB、BC、CC1、C1D1的中点.证明:FE、HG、DC三线共点.