题目内容
已知过椭圆
+y2=1(a>1)的顶点B(0,-1),做椭圆的弦AB,求|AB|的最大值,并求此时的A的坐标.
| x2 |
| a2 |
考点:直线与圆锥曲线的关系
专题:圆锥曲线中的最值与范围问题
分析:由点A是椭圆
+y2=1(a>1)上的一点,可设A(acosθ,sinθ)(θ∈[0,2π)).利用两点之间的距离公式可得|AB|2=(acosθ)2+(sinθ+1)2=(1-a2)(sinθ-
)2+1+a2-
.对a分类讨论利用二次函数的单调性即可得出.
| x2 |
| a2 |
| 1 |
| a2-1 |
| 1 |
| 1-a2 |
解答:
解:由点A是椭圆
+y2=1(a>1)上的一点,
可设A(acosθ,sinθ)(θ∈[0,2π)).
∴|AB|2=(acosθ)2+(sinθ+1)2
=a2cos2θ+sin2θ+2sinθ+1
=(1-a2)(sinθ-
)2+1+a2-
.
当1<a2<2时,
>1,当sinθ=1时,|AB|2取得最大值4,即AB|取得最大值2,此时A(0,1).
当a2≥2时,0<
≤1,当sinθ=
时,|AB|2取得最大值1+a2-
,即AB|取得最大值
,此时A(
,
).
| x2 |
| a2 |
可设A(acosθ,sinθ)(θ∈[0,2π)).
∴|AB|2=(acosθ)2+(sinθ+1)2
=a2cos2θ+sin2θ+2sinθ+1
=(1-a2)(sinθ-
| 1 |
| a2-1 |
| 1 |
| 1-a2 |
当1<a2<2时,
| 1 |
| a2-1 |
当a2≥2时,0<
| 1 |
| a2-1 |
| 1 |
| a2-1 |
| 1 |
| 1-a2 |
a2
| ||
| a2-1 |
±a
| ||
| a2-1 |
| 1 |
| a2-1 |
点评:本题考查了椭圆的参数方程、两点之间的距离公式、同角三角函数的基本关系式、二次函数的单调性,考查了分类讨论的思想方法,考查了推理能力 与计算能力,属于难题.

练习册系列答案
相关题目
若log2x•log34•log59=8,则x=( )
| A、8 | B、25 | C、16 | D、4 |
在△ABC中,下列各表达式为常数的是( )
| A、sin(A+B)+sinC | ||||||
| B、cos(B+C)-cosA | ||||||
C、tan
| ||||||
D、cos
|
设函数f(x)=x-
,对任意x∈[1,+∞),f(mx)+mf(x)>0恒成立,则实数m的取值范围是( )
| 1 |
| x |
| A、(-∞,-1)∪(1,+∞) |
| B、(1,+∞) |
| C、(-∞,-1) |
| D、不能确定 |
过正棱台两底面中心的截面一定是( )
| A、直角梯形 | B、等腰梯形 |
| C、一般梯形或等腰梯形 | D、矩形 |
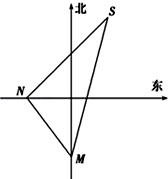 如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20海里,随后货轮按北偏西30°的方向航行30分钟到达N处后,又测得灯塔在货轮的东北方向,则货轮的速度为
如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20海里,随后货轮按北偏西30°的方向航行30分钟到达N处后,又测得灯塔在货轮的东北方向,则货轮的速度为