题目内容
不用计算器,求下列各式的值.
(1)64
-(-
)0+[(-2)3]
+(0.01) -
;
(2)lg200+
lg25+5(lg2+lg5)2+21-log23.
(1)64
| 1 |
| 3 |
| 5 |
| 9 |
| 4 |
| 3 |
| 1 |
| 2 |
(2)lg200+
| 1 |
| 2 |
考点:对数的运算性质,根式与分数指数幂的互化及其化简运算
专题:计算题
分析:根据指数的运算性质和对数的运算性质求解即可.
解答:
(本题满分12分)计算下列各式:
解:(1)原式=4-1+(-2)4+10
=29…(6分)
(2)∵lg200=2+lg2,
lg25=lg5,
5(lg2+lg5)2=5,
21-log23=2•2-log23=2•(2log23)-1=
∴原式=2+lg2+lg5+5+
=8+
=
…(12分)
解:(1)原式=4-1+(-2)4+10
=29…(6分)
(2)∵lg200=2+lg2,
| 1 |
| 2 |
5(lg2+lg5)2=5,
21-log23=2•2-log23=2•(2log23)-1=
| 2 |
| 3 |
∴原式=2+lg2+lg5+5+
| 2 |
| 3 |
| 2 |
| 3 |
| 26 |
| 3 |
点评:本题主要考查指数和对数的运算性质,属于基础题.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
下列不等式中:
①x2+3x-2>0和x2+3x-4>0;
②4x+
>8+
和4x>8;
③4x+
>8+
和4x>8;
④
>0和(x+3)(2-x)>0;
不等价的是( )
①x2+3x-2>0和x2+3x-4>0;
②4x+
| 5 |
| x+3 |
| 5 |
| x+3 |
③4x+
| 5 |
| x-3 |
| 5 |
| x-3 |
④
| x+3 |
| 2-x |
不等价的是( )
| A、①和② | B、①和③ |
| C、②和③ | D、②、③和④ |
设函数f(x)=x-
,对任意x∈[1,+∞),f(mx)+mf(x)>0恒成立,则实数m的取值范围是( )
| 1 |
| x |
| A、(-∞,-1)∪(1,+∞) |
| B、(1,+∞) |
| C、(-∞,-1) |
| D、不能确定 |
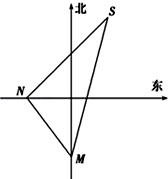 如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20海里,随后货轮按北偏西30°的方向航行30分钟到达N处后,又测得灯塔在货轮的东北方向,则货轮的速度为
如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20海里,随后货轮按北偏西30°的方向航行30分钟到达N处后,又测得灯塔在货轮的东北方向,则货轮的速度为