题目内容
17.已知等比数列{an}满足an>0,且a5•a2n-5=22n(n≥3),求数列{log2an}的前n项和Sn.分析 由数列{an}为等比数列且a5•a2n-5=22n(n≥3),可得$a_n^2={2^{2n}}$,又an>0,可得an.再利用对数的运算性质、等差数列的求和公式即可得出.
解答 解:由数列{an}为等比数列且a5•a2n-5=22n(n≥3),可得$a_n^2={2^{2n}}$,
又an>0,所以${a_n}={2^n}$.
则${S_n}={log_2}{a_1}+{log_2}{a_2}+…+{log_2}{a_n}={log_2}({a_1}{a_2}…{a_n})={log_2}{2^{1+2+…+n}}$
=1+2+…+n=$\frac{n(n+1)}{2}$.
点评 本题考查了等差数列与等比数列的通项公式与求和公式及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
8.若双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的渐近线将圆x2+y2-2x-4y+4=0平分,则双曲线的离心率为( )
| A. | 3 | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
5.如图所示,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的体积为( )


| A. | 12 | B. | 14 | C. | 16 | D. | 18 |
2.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+x+a,}&{x<0}\\{\frac{1}{x},}&{x>0}\end{array}\right.$的图象上存在不同的两点A、B,使得曲线y=f(x)在这两点处的切线重合,则实数a的取值范围是( )
| A. | ($\frac{1}{4}$,+∞) | B. | (2,+∞) | C. | (-∞,2) | D. | (-1,$\frac{1}{4}$) |
9.在封闭直三棱柱ABC-A1B1C1内有一个体积为V的球,若AB⊥BC,AB=15,BC=8,AA1=5,则V的最大值是( )
| A. | $\frac{9π}{2}$ | B. | $\frac{125π}{6}$ | C. | $\frac{32π}{3}$ | D. | 36π |
6.某企业想通过做广告来提高销售额,经预测可知本企业产品的广告费x(单位:百万元)与销售额y(单位:百万元)之间有如下对应数据:
由表中的数据得线性回归方程为$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,其中$\widehat{b}$=6.5,由此预测当广告费为7百万元时,销售额为6300万元.
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
11.已知函数f(x)=x3 的切线的斜率为12,则这样的切线有( )
| A. | 1条 | B. | 2条 | C. | 多余2条 | D. | 不确定 |
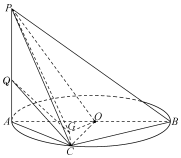 如图,点C在以AB为直径的圆O上,PA垂直与圆O所在平面,G为△AOC的垂心.
如图,点C在以AB为直径的圆O上,PA垂直与圆O所在平面,G为△AOC的垂心.