题目内容
2.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+x+a,}&{x<0}\\{\frac{1}{x},}&{x>0}\end{array}\right.$的图象上存在不同的两点A、B,使得曲线y=f(x)在这两点处的切线重合,则实数a的取值范围是( )| A. | ($\frac{1}{4}$,+∞) | B. | (2,+∞) | C. | (-∞,2) | D. | (-1,$\frac{1}{4}$) |
分析 先根据导数的几何意义写出函数f(x)在点A、B处的切线方程,再利用两直线重合的充要条件:斜率相等且纵截距相等,列出关系式,从而得出a=$\frac{1}{4}$(t4+2t2+8t+1),t>0,由单调性可得出a的取值范围.
解答 解:当x<0时,f(x)=x2+x+a的导数为f′(x)=2x+1;
当x>0时,f(x)=$\frac{1}{x}$的导数为f′(x)=-$\frac{1}{{x}^{2}}$,
设A(x1,f(x1)),B(x2,f(x2))为该函数图象上的两点,且x1<x2,
当x1<x2<0,或0<x1<x2时,f′(x1)≠f′(x2),故x1<0<x2,
当x1<0时,函数f(x)在点A(x1,f(x1))处的切线方程为:
y-(x12+x1+a)=(2x1+1)(x-x1);
当x2>0时,函数f(x)在点B(x2,f(x2))处的切线方程为y-$\frac{1}{{x}_{2}}$=-$\frac{1}{{{x}_{2}}^{2}}$(x-x2).
两直线重合的充要条件是-$\frac{1}{{{x}_{2}}^{2}}$=2x1+1①,$\frac{2}{{x}_{2}}$=a-x12②,
由x1<0<x2得0<$\frac{1}{{x}_{2}}$<1,
由①②令t=$\frac{1}{{x}_{2}}$,则t>0,且a=$\frac{1}{4}$(t4+2t2+8t+1)在(0,+∞)为增函数,
∴a>$\frac{1}{4}$,
故选:A.
点评 本题主要考查了导数的几何意义等基础知识,考查了推理论证能力、运算能力、创新意识,考查了函数与方程、分类与整合、转化与化归等思想方法.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
12.我国古代名著《九章算术》中有这样一段话:“今有金锤,长五尺,斩本一尺,重四斤.斩末一尺,重二斤.”意思是:“现有一根金锤,头部的1尺,重4斤;尾部的1尺,重2斤;且从头到尾,每一尺的重量构成等差数列.”则下列说法错误的是( )
| A. | 该金锤中间一尺重3斤 | |
| B. | 中间三尺的重量和是头尾两尺重量和的3倍 | |
| C. | 该金锤的重量为15斤 | |
| D. | 该金锤相邻两尺的重量之差的绝对值为0.5斤 |
10.曲线y=lgx在x=1处的切线斜率是( )
| A. | $\frac{1}{ln10}$ | B. | ln10 | C. | lne | D. | $\frac{1}{lne}$ |
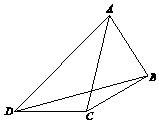 在如图所示的平面图形中,已知CD=$\sqrt{2}$,∠BCA=45°,∠ACD=105°,∠CDB=15°,∠BDA=30°.
在如图所示的平面图形中,已知CD=$\sqrt{2}$,∠BCA=45°,∠ACD=105°,∠CDB=15°,∠BDA=30°.