题目内容
7.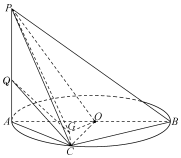 如图,点C在以AB为直径的圆O上,PA垂直与圆O所在平面,G为△AOC的垂心.
如图,点C在以AB为直径的圆O上,PA垂直与圆O所在平面,G为△AOC的垂心.(1)求证:平面OPG⊥平面PAC;
(2)若PA=AB=2AC=2,点Q在线段PA上,且PQ=2QA,求三棱锥P-QGC的体积.
分析 (1)由OG⊥AC,OG⊥PA即可得出OG⊥平面PAC,故而平面OPG⊥平面PAC;
(2)利用公式VP-QGC=VG-PQC=$\frac{1}{3}{S}_{△PQC}$•GM计算体积.
解答 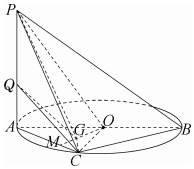 (1)证明:∵G为△AOC的垂心,∴OG⊥AC,
(1)证明:∵G为△AOC的垂心,∴OG⊥AC,
∵PA⊥平面ABC,OG?平面ABC,
∴PA⊥OG.
又PA?平面PAC,AC?平面PAC,PA∩AC=A,
∴OG⊥平面PAC.
又OG?平面OPG,
∴平面OPG⊥平面PAC.
(2)解:延长OG交AC于点M.
由(1)知OM⊥平面PAC,
即GM为点G到平面PAC的距离.
由已知可得,OA=OC=AC=1,
∴△AOC为正三角形,
∴$OM=\frac{{\sqrt{3}}}{2}$.$GM=\frac{1}{3}OM=\frac{{\sqrt{3}}}{6}$.
∵PA=2,PQ=2QA,∴PQ=$\frac{4}{3}$.
∴S△PQC=$\frac{1}{2}PQ•CA$=$\frac{1}{2}×\frac{4}{3}×1$=$\frac{2}{3}$,
∴VP-QGC=VG-PQC=$\frac{1}{3}{S}_{△PQC}$•GM=$\frac{1}{3}×\frac{2}{3}$×$\frac{{\sqrt{3}}}{6}=\frac{{\sqrt{3}}}{27}$.
点评 本题考查了面面垂直的判定,棱锥的体积计算,属于中档题.

练习册系列答案
相关题目
17.已知△ABC的内角A,B,C所对的边分别为a,b,c,a=15,b=10,A=60°,则sinB等于( )
| A. | -$\frac{\sqrt{6}}{3}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | -$\frac{\sqrt{3}}{3}$ |
15.已知集合A={x∈N|-2<x<4},$B=\{x|\frac{1}{2}≤{2^x}≤4\}$,则A∩B=( )
| A. | {x|-1≤x≤2} | B. | {-1,0,1,2} | C. | {1,2} | D. | {0,1,2} |
12.我国古代名著《九章算术》中有这样一段话:“今有金锤,长五尺,斩本一尺,重四斤.斩末一尺,重二斤.”意思是:“现有一根金锤,头部的1尺,重4斤;尾部的1尺,重2斤;且从头到尾,每一尺的重量构成等差数列.”则下列说法错误的是( )
| A. | 该金锤中间一尺重3斤 | |
| B. | 中间三尺的重量和是头尾两尺重量和的3倍 | |
| C. | 该金锤的重量为15斤 | |
| D. | 该金锤相邻两尺的重量之差的绝对值为0.5斤 |
19.已知集合A={x|x<a},B={x|x2-3x+2<0},若A∩B=B,则实数a的取值范围是( )
| A. | a≤1 | B. | a<1 | C. | a≥2 | D. | a>2 |
16.在一次实验中,同时抛掷4枚均匀的硬币16次,设4枚硬币正好出现3枚正面向上,1枚反面向上的次数为ξ,则ξ的方差是( )
| A. | 3 | B. | 4 | C. | 1 | D. | $\frac{15}{16}$ |