题目内容
8.若双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的渐近线将圆x2+y2-2x-4y+4=0平分,则双曲线的离心率为( )| A. | 3 | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
分析 根据题意,由双曲线的方程分析可得其渐近线方程,由圆的方程分析可得圆的圆心坐标,由题意分析可得双曲线的渐近线将圆x2+y2-2x-4y+4=0平分,则直线y=$\frac{b}{a}$x过圆心,即可得有$\frac{b}{a}$=2,即b=2a,由双曲线的几何性质可得c的值,由双曲线离心率公式计算可得答案.
解答 解:根据题意,双曲线的方程为$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$,
则其渐近线方程为y=±$\frac{b}{a}$x,
圆x2+y2-2x-4y+4=0,其标准方程为:(x-1)2+(y-2)2=1,其圆心为(1,2),
若双曲线的渐近线将圆x2+y2-2x-4y+4=0平分,则直线y=$\frac{b}{a}$x过圆心,
则有$\frac{b}{a}$=2,即b=2a,
则c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{5}$a,
则其离心率e=$\frac{c}{a}$=$\sqrt{5}$;
故选:B.
点评 本题考查双曲线的几何性质,注意渐近线将圆x2+y2-2x-4y+4=0平分,即渐近线过圆的圆心.

练习册系列答案
相关题目
19.已知集合A={x|x<a},B={x|x2-3x+2<0},若A∩B=B,则实数a的取值范围是( )
| A. | a≤1 | B. | a<1 | C. | a≥2 | D. | a>2 |
16.在一次实验中,同时抛掷4枚均匀的硬币16次,设4枚硬币正好出现3枚正面向上,1枚反面向上的次数为ξ,则ξ的方差是( )
| A. | 3 | B. | 4 | C. | 1 | D. | $\frac{15}{16}$ |
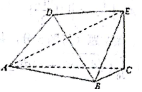 如图,以A、B、C、D、E为顶点的六面体中,△ABC和△ABD均为等边三角形,且平面ABC⊥平面ABD,EC⊥平面ABC,EC=$\sqrt{3}$,AB=2.
如图,以A、B、C、D、E为顶点的六面体中,△ABC和△ABD均为等边三角形,且平面ABC⊥平面ABD,EC⊥平面ABC,EC=$\sqrt{3}$,AB=2.