题目内容
已知函数f(x)=|lnx|,若
>a>b>1,则f(a),f(b),f(c)比较大小关系正确的是( )
| 1 |
| c |
| A、f(c)>f(b)>f(a) |
| B、f(b)>f(c)>f(a) |
| C、f(c)>f(a)>f(b) |
| D、f(b)>f(a)>f(c) |
考点:对数的运算性质
专题:函数的性质及应用
分析:由
>a>b>1得出ln
>lna>lnb>0,再由ln
=-lnc,得出|lnc|=|ln
|;即可判定f(a),f(b),f(c)的大小关系.
| 1 |
| c |
| 1 |
| c |
| 1 |
| c |
| 1 |
| c |
解答:
解:∵函数f(x)=|lnx|,
且
>a>b>1时,ln
>lna>lnb>0;
∴|ln
|>|lna|>|lnb|>0;
又ln
=-lnc,
∴|lnc|=|ln
|;
即|lnc|>|lna|>|lnb|;
∴f(c)>f(a)>f(b).
故选:C.
且
| 1 |
| c |
| 1 |
| c |
∴|ln
| 1 |
| c |
又ln
| 1 |
| c |
∴|lnc|=|ln
| 1 |
| c |
即|lnc|>|lna|>|lnb|;
∴f(c)>f(a)>f(b).
故选:C.
点评:本题考查了利用对数函数的图象与性质判定对数值大小的问题,解题时应熟练地掌握对数函数的图象与性质以及对数的运算法则,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
某几何体的三视图如图所示,则该几何体的体积为( )
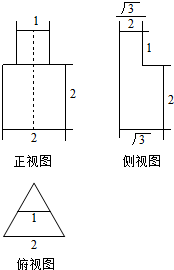

A、3
| ||||
B、
| ||||
C、
| ||||
D、
|
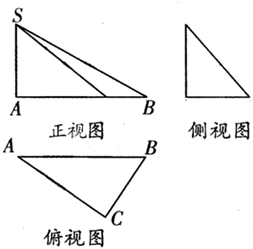 已知三棱锥S-ABC的三视图如图所示,其中俯视图中AC⊥BC,在原三棱锥中给出下列命题:①BC⊥平面SAC;②平面SBC⊥平面SAB;③SB⊥AC.其中所有正确命题是( )
已知三棱锥S-ABC的三视图如图所示,其中俯视图中AC⊥BC,在原三棱锥中给出下列命题:①BC⊥平面SAC;②平面SBC⊥平面SAB;③SB⊥AC.其中所有正确命题是( )| A、①② | B、①③ | C、② | D、① |
命题p:?x∈R,x2-2x+
e2xdx>0,则( )
| ∫ | 1 0 |
A、p是真命题,¬p:?x∈R,x2-2x+
| ||
B、p是假命题,¬p:?x∈R,x2-2x+
| ||
C、p是真命题,¬p:?x∈R,x2-2x+
| ||
D、p是假命题,¬p:?x∈R,x2-2x+
|
某几何体的三视图如图所示,则该几何体的体积是( )
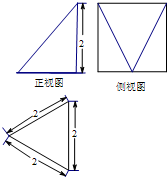

A、
| ||||
B、
| ||||
C、2
| ||||
D、4
|
