题目内容
已知曲线y=ln
过点M(1,b),且在点M处的切线与直线x-3y-2=0垂直.
(1)求a,b的值;
(2)求曲线在点M处的切线与两坐标轴围成的三角形的面积.
| 1 |
| 3x-a |
(1)求a,b的值;
(2)求曲线在点M处的切线与两坐标轴围成的三角形的面积.
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)求函数的导数,根据导数的几何意义即可求a,b的值;
(2)求曲线在点M处的切线,以及两坐标轴的交点坐标即可求三角形的面积.
(2)求曲线在点M处的切线,以及两坐标轴的交点坐标即可求三角形的面积.
解答:
解:(1)直线x-3y-2=0的斜率k=
,则切线斜率k=-3,
即函数的f′(1)=-3,
∵y=ln
,
∴函数的导数f′(x)=3(3x-a)•(-
)=-
即f′(1)=-
=-3,解得a=2,
即函数为f(x)=ln
,则b=ln1=0,
即a=2,b=0;
(2)∵b=0,∴M(1,0),
则曲线在点M处的切线为y=-3(x-1),
当x=0,解得y=3,
当y=0,解得x=1,
则切线与两坐标轴围成的三角形的面积S=
×1×3=
.
| 1 |
| 3 |
即函数的f′(1)=-3,
∵y=ln
| 1 |
| 3x-a |
∴函数的导数f′(x)=3(3x-a)•(-
| 1 |
| (3x-a)2 |
| 3 |
| 3x-a |
即f′(1)=-
| 3 |
| 3-a |
即函数为f(x)=ln
| 1 |
| 3x-2 |
即a=2,b=0;
(2)∵b=0,∴M(1,0),
则曲线在点M处的切线为y=-3(x-1),
当x=0,解得y=3,
当y=0,解得x=1,
则切线与两坐标轴围成的三角形的面积S=
| 1 |
| 2 |
| 3 |
| 2 |
点评:本题主要考查导数的几何意义以及切线方程的求解,求函数的导数是解决本题的关键.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
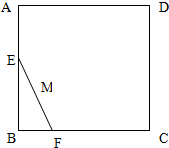 如图,线段EF的长度为1,端点E、F在边长不小于1的正方形ABCD的四边上滑动,当E、F沿着正方形的四边滑动一周时,EF的中点M所形成的轨迹为G,若G的周长为L,其围成的面积为S,则L-S的最大值为( )
如图,线段EF的长度为1,端点E、F在边长不小于1的正方形ABCD的四边上滑动,当E、F沿着正方形的四边滑动一周时,EF的中点M所形成的轨迹为G,若G的周长为L,其围成的面积为S,则L-S的最大值为( )| A、4-π | ||
B、2+
| ||
C、
| ||
| D、2π-2 |
已知某几何体的三视图如上图所示(单位:cm),则该几何体的表面积是( )
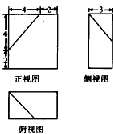

A、(124+2
| ||
| B、92cm2 | ||
| C、124cm2 | ||
| D、84cm2 |