题目内容
设
、
、
为平面向量,下面的命题中:
①
•(
-
)=
•
-
•
;
②(
•
)•
=
•(
•
);
③(
-
)2=|
|2-2|
|•|
|+|
|2;
④若
•
=0,则
=
或
=
.
正确的个数是( )
| a |
| b |
| c |
①
| a |
| b |
| c |
| a |
| b |
| a |
| c |
②(
| a |
| b |
| c |
| a |
| b |
| c |
③(
| a |
| b |
| a |
| a |
| b |
| b |
④若
| a |
| b |
| a |
| 0 |
| b |
| 0 |
正确的个数是( )
| A、3 | B、2 | C、1 | D、0 |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:①利用向量的分配律可知,正确;
②由于
•
与
•
为实数,而
与
不一定共线,即可判断出;
③利用向量的运算性质可得(
-
)2=
2-2
•
+
2,而
•
≤|
| |
|,即可判断出;
④若
•
=0,则
=
或
=
或
⊥
,即可得出.
②由于
| a |
| b |
| b |
| c |
| c |
| a |
③利用向量的运算性质可得(
| a |
| b |
| a |
| a |
| b |
| b |
| a |
| b |
| a |
| b |
④若
| a |
| b |
| a |
| 0 |
| b |
| 0 |
| a |
| b |
解答:
解:①利用向量的分配律可知:
•(
-
)=
•
-
•
,正确;
②∵
•
与
•
为实数,而
与
不一定共线,因此不正确;
③利用向量的运算性质可得(
-
)2=
2-2
•
+
2,而
•
≤|
| |
|,因此不正确;
④若
•
=0,则
=
或
=
或
⊥
,因此不正确.
综上可知:正确的个数是1.
故选:C.
| a |
| b |
| c |
| a |
| b |
| a |
| c |
②∵
| a |
| b |
| b |
| c |
| c |
| a |
③利用向量的运算性质可得(
| a |
| b |
| a |
| a |
| b |
| b |
| a |
| b |
| a |
| b |
④若
| a |
| b |
| a |
| 0 |
| b |
| 0 |
| a |
| b |
综上可知:正确的个数是1.
故选:C.
点评:本题综合考查了向量的运算及其性质,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图是一个体积为10的空间几何体的三视图,则图中x的值为( )


| A、2 | B、3 | C、4 | D、5 |
设Sn为等差数列{an}的前n项和.若a4<0,a5>|a4|,则使Sn>0成立的最小正整数n为( )
| A、6 | B、7 | C、8 | D、9 |
已知数列{an}是等比数列,且an>0,若bn=log2an,则( )
| A、{bn}一定是递增的等差数列 |
| B、{bn}不可能是等比数列 |
| C、{2b2n-1+1}是等差数列 |
| D、{3bn}不是等比数列 |
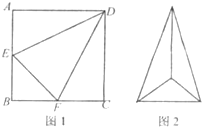 如图1,边长为2的d正方形ABCD中,E,F 分别是AB,BC的中点,将△ADE,△CDF,△BEF折起,使A,C,B二点重合于G,所得二棱锥G-DEF的俯视图如图2,则其正视图的面积为
如图1,边长为2的d正方形ABCD中,E,F 分别是AB,BC的中点,将△ADE,△CDF,△BEF折起,使A,C,B二点重合于G,所得二棱锥G-DEF的俯视图如图2,则其正视图的面积为 如图,PA,PB是圆O的两条切线,A,B是切点,C是劣弧AB(不包括端点)上一点,直线PC交圆O于另一点D,Q在弦CD上,且∠DAQ=∠PBC.求证:
如图,PA,PB是圆O的两条切线,A,B是切点,C是劣弧AB(不包括端点)上一点,直线PC交圆O于另一点D,Q在弦CD上,且∠DAQ=∠PBC.求证: