题目内容
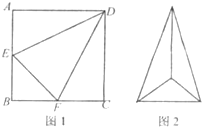 如图1,边长为2的d正方形ABCD中,E,F 分别是AB,BC的中点,将△ADE,△CDF,△BEF折起,使A,C,B二点重合于G,所得二棱锥G-DEF的俯视图如图2,则其正视图的面积为
如图1,边长为2的d正方形ABCD中,E,F 分别是AB,BC的中点,将△ADE,△CDF,△BEF折起,使A,C,B二点重合于G,所得二棱锥G-DEF的俯视图如图2,则其正视图的面积为考点:简单空间图形的三视图
专题:空间位置关系与距离
分析:判断正视图的形状,先求几何体的高,几何体的高即为正视图的高,再求底边长,代入面积公式计算.
解答:
解:过G作GO⊥平面DEF,垂足为O,如图:
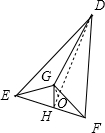
∵E,F 分别是AB,BC的中点,∴DG=2,EF=
,△EFG为等腰直角三角形,∴GH=
,
∵DG⊥平面EFG,GH?平面EFG,∴DG⊥GH,
在Rt△DGH中,DH=
,∴GO=
=
,
几何体的正视图是以EF为底边,GO为高的三角形,
∴正视图的面积为
×
×
=
.
故答案为:
.

∵E,F 分别是AB,BC的中点,∴DG=2,EF=
| 2 |
| ||
| 2 |
∵DG⊥平面EFG,GH?平面EFG,∴DG⊥GH,
在Rt△DGH中,DH=
3
| ||
| 2 |
2×
| ||||
|
| 2 |
| 3 |
几何体的正视图是以EF为底边,GO为高的三角形,
∴正视图的面积为
| 1 |
| 2 |
| 2 |
| 2 |
| 3 |
| ||
| 3 |
故答案为:
| ||
| 3 |
点评:本题考查了几何图形的三视图,正视图是从几何体的正面看几何体所得图形,解答本题的关键是求正视图的高.

练习册系列答案
相关题目
 如图是一个几何体的三视图,若它的体积为2,则a+b的最小值为
如图是一个几何体的三视图,若它的体积为2,则a+b的最小值为 如图,四面体ABCD中,点A在平面BCD上的射影O在BD上,点M、N分别是BC、BD的中点,AM与平面BCD成45°角,BC⊥CD,∠BDC=30°,BC=2,BO=1
如图,四面体ABCD中,点A在平面BCD上的射影O在BD上,点M、N分别是BC、BD的中点,AM与平面BCD成45°角,BC⊥CD,∠BDC=30°,BC=2,BO=1