题目内容
12.下列函数中,既是奇函数又在区间(0,+∞)上为增函数的是( )| A. | y=lnx | B. | y=x3 | C. | y=x2 | D. | y=sinx |
分析 根据奇函数图象的对称性,奇函数、偶函数的定义,以及正弦函数的单调性便可判断每个选项的正误,从而找出正确选项.
解答 解:A.y=lnx的图象不关于原点对称,不是奇函数,∴该选项错误;
B.y=x3为奇函数,x增大时,x3增大,即y增大,∴该函数在(0,+∞)上为增函数,∴该选项正确;
C.y=x2是偶函数,不是奇函数,∴该选项错误;
D.y=sinx在(0,+∞)上没有单调性,∴该选项错误.
故选:B.
点评 考查奇函数图象的对称性,奇函数、偶函数的定义,以及正弦函数的单调性,要清楚每个选项的函数的图象.

练习册系列答案
相关题目
3.若角α的顶点为坐标原点,始边与x轴的非负半轴重合,且终边上一点的坐标为(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),则tanα的值为( )
| A. | -$\sqrt{3}$ | B. | -$\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{1}{2}$ |
17.如图,在平行四边形ABCD中,E为BC的中点,且$\overrightarrow{DE}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$,则( )
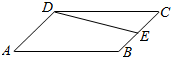

| A. | x=-1,y=-$\frac{1}{2}$ | B. | x=1,y=$\frac{1}{2}$ | C. | x=-1,y=$\frac{1}{2}$ | D. | x=1,y=-$\frac{1}{2}$ |
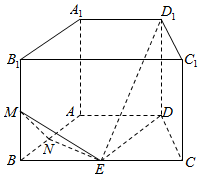 如图,直四棱柱ABCD-A1B1C1D1的底面是等腰梯形,AB=CD=AD=1,BC=2,E,M,N分别是所在棱的中点.
如图,直四棱柱ABCD-A1B1C1D1的底面是等腰梯形,AB=CD=AD=1,BC=2,E,M,N分别是所在棱的中点.