题目内容
7.已知定义在R上的奇函数f (x)满足f(x)=f(4-x),且在区间[0,2]上是增函数,那么( )| A. | f(6)<f(4)<f(1) | B. | f(4)<f(6)<f(1) | C. | f(1)<f(6)<f(4) | D. | f(6)<f(1)<f(4) |
分析 根据函数奇偶性和单调性的关系将条件进行转化比较即可.
解答 解:∵f(x)=f(4-x),
∴函数f(x)关于x=2对称,
则∵奇函数f (x)在区间[0,2]上是增函数,
∴函数f(x)在区间[-2,2]上是增函数,
则函数f(x)在在区间[2,6]上是减函数,
则f(1)=f(3),
∵f(6)<f(4)<f(3),
∴f(6)<f(4)<f(1),
故选:A
点评 本题主要考查函数值的大小比较,根据函数奇偶性和对称性的性质将条件进行转化是解决本题的关键.

练习册系列答案
相关题目
15.已知直线l:y=kx+2k+1与抛物线C:y2=4x,若l与C有且仅有一个公共点,则实数k的取值集合为( )
| A. | $\left\{{-1,\frac{1}{2}}\right\}$ | B. | {-1,0} | C. | $\left\{{-1,0,\frac{1}{2}}\right\}$ | D. | $\left\{{0,\frac{1}{2}}\right\}$ |
12.过点(2,-1)且倾斜角为60°的直线方程为( )
| A. | $\sqrt{3}x-y-2\sqrt{3}$-1=0 | B. | $\sqrt{3}x-3y-2\sqrt{3}$-3=0 | C. | $\sqrt{3}x-y+2\sqrt{3}$+1=0 | D. | $\sqrt{3}x-3y+2\sqrt{3}+3=0$ |
19.函数f(x)的图象如图所示,则下列结论正确的是( )
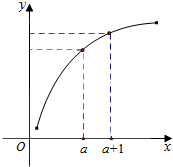

| A. | 0<f′(a)<f′(a+1)<f(a+1)-f(a) | B. | 0<f′(a+1)<f(a+1)-f(a)<f′(a) | ||
| C. | 0<f′(a+1)<f′(a)<f(a+1)-f(a) | D. | 0<f(a+1)-f(a)<f′(a)<f′(a+1) |
16.已知集合A={x|0<x<3},B=$\left\{{x|y=\sqrt{{x^2}-1}}\right\}$,则集合A∩(∁RB)为( )
| A. | [0,1) | B. | (0,1) | C. | [1,3) | D. | (1,3) |
17.如图,在平行四边形ABCD中,E为BC的中点,且$\overrightarrow{DE}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$,则( )
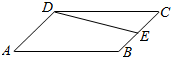

| A. | x=-1,y=-$\frac{1}{2}$ | B. | x=1,y=$\frac{1}{2}$ | C. | x=-1,y=$\frac{1}{2}$ | D. | x=1,y=-$\frac{1}{2}$ |