题目内容
已知函数f(x)=x-a,g(x)=a-
(a∈R).
(Ⅰ)判断函数h(x)=f(x)-g(x)在x∈[1,4]的单调性并用定义证明;
(Ⅱ)令F(x)=|f(x)|+g(x),求F(x)在区间x∈[1,4]的最大值的表达式M(a).
| 1 |
| x |
(Ⅰ)判断函数h(x)=f(x)-g(x)在x∈[1,4]的单调性并用定义证明;
(Ⅱ)令F(x)=|f(x)|+g(x),求F(x)在区间x∈[1,4]的最大值的表达式M(a).
考点:利用导数研究函数的单调性,函数的最值及其几何意义
专题:函数的性质及应用
分析:(Ⅰ)利用函数单调性的定义证明即可.
(2)根据定义的M(a)为f(x)的最大值,写出不同区间上的表示式,根据不同区间上的表示式,写出分段函数.
(2)根据定义的M(a)为f(x)的最大值,写出不同区间上的表示式,根据不同区间上的表示式,写出分段函数.
解答:
解:(Ⅰ)∵f(x)=x-a,g(x)=a-
,
∴h(x)=f(x)-g(x)=x+
,
设x1,x2∈[1,4],且x1<x2,
则f(x2)-f(x1)=(x2+
)-(x1+
)=
,
∵x1,x2∈[1,4],且x1<x2,
∴x2-x1>0,x1x2>0,x1x2-1>0,
∴f(x2)-f(x1)>0,
∴h(x)=f(x)-g(x)在x∈[1,4]的单调递增,
(Ⅱ)∵F(x)=|f(x)|+g(x)=|x-a|+a-
,
当a≤0时,
F(x)=x-
,在x∈[1,4]的单调递增,M(a)=
,
当a≥4时,
F(x)=2a-(x+
),在x∈[1,4]的单调递减,M(a)=2a-2,
当0<a<4时
①a≤x≤4时,F(x)=x-
,在x∈[1,4]的单调递增,M(a)=
,
②1≤x<a时,F(x)=2a-(x+
),在x∈[1,4]的单调递减,M(a)=2a-2,
综上所述,M(a)=
.
| 1 |
| x |
∴h(x)=f(x)-g(x)=x+
| 1 |
| x |
设x1,x2∈[1,4],且x1<x2,
则f(x2)-f(x1)=(x2+
| 1 |
| x2 |
| 1 |
| x1 |
| (x2-x1)(x1x2-1) |
| x1x2 |
∵x1,x2∈[1,4],且x1<x2,
∴x2-x1>0,x1x2>0,x1x2-1>0,
∴f(x2)-f(x1)>0,
∴h(x)=f(x)-g(x)在x∈[1,4]的单调递增,
(Ⅱ)∵F(x)=|f(x)|+g(x)=|x-a|+a-
| 1 |
| x |
当a≤0时,
F(x)=x-
| 1 |
| x |
| 15 |
| 4 |
当a≥4时,
F(x)=2a-(x+
| 1 |
| x |
当0<a<4时
①a≤x≤4时,F(x)=x-
| 1 |
| x |
| 15 |
| 4 |
②1≤x<a时,F(x)=2a-(x+
| 1 |
| x |
综上所述,M(a)=
|
点评:本题考查利用定义判断函数的单调性,本题解题的关键是看清题干中所给的条件,写出正确的单调区间.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
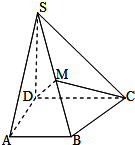 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠DAB=90°,AB∥CD,AD=CD=2AB=2,E,F分别是PC,CD的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠DAB=90°,AB∥CD,AD=CD=2AB=2,E,F分别是PC,CD的中点. 设函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<
设函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<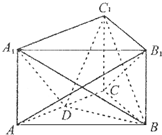 如图所示,在三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,且底面是边长为2的正三角形,侧棱长为1,D是AC的中点.
如图所示,在三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,且底面是边长为2的正三角形,侧棱长为1,D是AC的中点.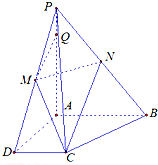 已知四棱锥P-ABCD中,PA⊥平面ABCD,且PA=4,底面为直角梯形,∠CDA=∠BAD=90°,AB=2,CD=1,AD=
已知四棱锥P-ABCD中,PA⊥平面ABCD,且PA=4,底面为直角梯形,∠CDA=∠BAD=90°,AB=2,CD=1,AD=