题目内容
已知等差数列{an}的首项a1=1，公差d＞0，且第2项、第5项、第14项分别是等比数列{bn}的第2项、第3项、第4项．
（1）求数列{an}，{bn}的通项公式；
（2）若数列{cn}对任意n∈N*，均有
+
+…+
=an+1成立．
①求证：
=2（n≥2）；
②求c1+c2+…+c2014．
（1）求数列{an}，{bn}的通项公式；
（2）若数列{cn}对任意n∈N*，均有
| c1 |
| b1 |
| c2 |
| b2 |
| cn |
| bn |
①求证：
| cn |
| bn |
②求c1+c2+…+c2014．
考点：数列的求和,等差数列的性质,等比数列的性质
专题：
分析：（1）首先利用等差数列的通项公式将第2项，第5项，第14项用{an}的首项与公差表示，再根据此三项成等比数列，列出方程，求出公差，利用等差数列及等比数列的通项公式求出数列{an}与{bn}的通项公式即可；
（2）首先根据题意，再写一式，表示出an，然后两式相减，可推得
=2，进而求出数列{cn}的通项，最后求数列{cn}前2014项的和即可．
（2）首先根据题意，再写一式，表示出an，然后两式相减，可推得
| cn |
| bn |
解答：
解：（1）∵a2=1+d，a5=1+4d，a14=1+13d，
∴（1+4d）2=（1+d）（1+13d），
解得d=2（∵d＞0）∴an=1+（n-1）×2=2n-1；
又∵b2=a2=3，a5=b3=9，
所以等比数列{bn}的公比q=
=3，
∴bn=b2qn-2=3n-1
（2）①证明：∵
+
+…+
=an+1
∴当n≥2时，
+
+…+
=an
两式相减，得
=an+1-an=2(n≥2)．
②由①得cn=2bn=2×3n-1(n≥2)
当n=1时，
=a2，∴c1=3不满足上式
∴c1+c2+…+c2014=3+2×31+2×32+…+2×32013=3+
=3-3+32014=32014
∴（1+4d）2=（1+d）（1+13d），
解得d=2（∵d＞0）∴an=1+（n-1）×2=2n-1；
又∵b2=a2=3，a5=b3=9，
所以等比数列{bn}的公比q=
| b3 |
| b2 |
∴bn=b2qn-2=3n-1
（2）①证明：∵
| c1 |
| b1 |
| c2 |
| b2 |
| cn |
| bn |
∴当n≥2时，
| c1 |
| b1 |
| c2 |
| b2 |
| cn-1 |
| bn-1 |
两式相减，得
| cn |
| bn |
②由①得cn=2bn=2×3n-1(n≥2)
当n=1时，
| c1 |
| b1 |
∴c1+c2+…+c2014=3+2×31+2×32+…+2×32013=3+
| 6-6×32013 |
| 1-3 |
点评：本题主要考查了利用基本量表示等差数列、等比数列的通项，考查数列的求和，考查学生的计算能力．
练习册系列答案
相关题目
AB为圆O的直径，点E、F在圆上，AB∥EF，矩形ABCD所在平面与圆O所在平面互相垂直，已知AB=2，BC=EF=1
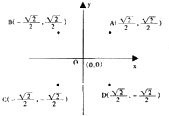如图，A（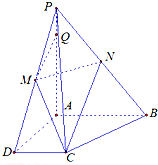
已知四棱锥P-ABCD中，PA⊥平面ABCD，且PA=4，底面为直角梯形，∠CDA=∠BAD=90°，AB=2，CD=1，AD=