题目内容
设f(x)=ln(x2+1),g(x)=
x2-
.
(1)求F(x)=f(x)-g(x)的单调区间,并证明对[-1,1]上的任意x1,x2,x3,都有F(x1)+F(x2)>F(x3);
(2)将y=f(x)的图象向下平移a(a>0)个单位,同时将y=g(x)的图象向上平移b(b>0)个单位,使它们恰有四个交点,求
的取值范围.
| 1 |
| 2 |
| 1 |
| 2 |
(1)求F(x)=f(x)-g(x)的单调区间,并证明对[-1,1]上的任意x1,x2,x3,都有F(x1)+F(x2)>F(x3);
(2)将y=f(x)的图象向下平移a(a>0)个单位,同时将y=g(x)的图象向上平移b(b>0)个单位,使它们恰有四个交点,求
| a+1 |
| b+1 |
考点:利用导数研究函数的单调性,函数的图象与图象变化
专题:导数的综合应用
分析:(1)由F′(x)=
-x=-
,得F(x)在(-∞,-1)和(0,1)上单调递增,在(-1,0)和(1,+∞)上单调递减,因此F(x1)+F(x2)≥2F(x)min=1,而F(x3)≤F(x)max=ln 2,故F(x1)+F(x2)>F(x3).
(2)由ln(x2+1)-a=
x2-
+b,则a+b=ln(x2+1)-
x2+
.令F(x)=ln(x2+1)-
x2+
,从而F(x)极小值=F(0)=
,F(x)极大值=F(1)=ln 2.
又F(4)=F(-4)<0<F(0),又
可视为点P(-1,-1)与可行域内的点连线的斜率,故
<
<1+ln 2.
| 2x |
| x2+1 |
| x(x+1)(x-1) |
| x2+1 |
(2)由ln(x2+1)-a=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又F(4)=F(-4)<0<F(0),又
| a+1 |
| b+1 |
| 1 |
| 1+ln2 |
| a+1 |
| b+1 |
解答:
解:(1)∵F(x)=ln(x2+1)-
x2-
,
∴F′(x)=
-x=-
.
F′(x),F(x)的值随x值的变化如下表:
故F(x)在(-∞,-1)和(0,1)上单调递增,在(-1,0)和(1,+∞)上单调递减,
在[-1,1]上F(x)的最小值F(x)min=F(0)=
.F(x)的最大值F(x)max=F(1)=F(-1)=ln 2.
因此F(x1)+F(x2)≥2F(x)min=1,而F(x3)≤F(x)max=ln 2,
故F(x1)+F(x2)>F(x3).
(2)由题意可知y=ln(x2+1)-a与y=
x2-
+b的图象恰有四个交点.
由ln(x2+1)-a=
x2-
+b,
则a+b=ln(x2+1)-
x2+
.
令F(x)=ln(x2+1)-
x2+
,
由(1)可知F(x)极小值=F(0)=
,F(x)极大值=F(1)=ln 2.
又F(4)=F(-4)<0<F(0),
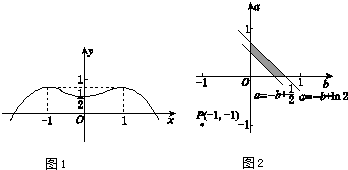
所以F(x)的大致图象如图(1)所示,
要使y=a+b与y=F(x)恰有四个交点,
则
<a+b<ln 2.由
得到(b,a)的可行域为如图(2)所示的阴部分.
又
可视为点P(-1,-1)与可行域内的点连线的斜率,
故
<
<1+ln 2.
| 1 |
| 2 |
| 1 |
| 2 |
∴F′(x)=
| 2x |
| x2+1 |
| x(x+1)(x-1) |
| x2+1 |
F′(x),F(x)的值随x值的变化如下表:
| x | (-∞,-1) | (-1,0) | (0,1) | (1,+∞) |
| F′(x) | + | - | + | - |
| F(x) | ↗ | ↘ | ↗ | ↘ |
在[-1,1]上F(x)的最小值F(x)min=F(0)=
| 1 |
| 2 |
因此F(x1)+F(x2)≥2F(x)min=1,而F(x3)≤F(x)max=ln 2,
故F(x1)+F(x2)>F(x3).
(2)由题意可知y=ln(x2+1)-a与y=
| 1 |
| 2 |
| 1 |
| 2 |
由ln(x2+1)-a=
| 1 |
| 2 |
| 1 |
| 2 |
则a+b=ln(x2+1)-
| 1 |
| 2 |
| 1 |
| 2 |
令F(x)=ln(x2+1)-
| 1 |
| 2 |
| 1 |
| 2 |
由(1)可知F(x)极小值=F(0)=
| 1 |
| 2 |
又F(4)=F(-4)<0<F(0),
所以F(x)的大致图象如图(1)所示,
要使y=a+b与y=F(x)恰有四个交点,
则
| 1 |
| 2 |
|
得到(b,a)的可行域为如图(2)所示的阴部分.
又
| a+1 |
| b+1 |
故
| 1 |
| 1+ln2 |
| a+1 |
| b+1 |

点评:本题考察了函数的单调性,导数的应用,不等式的证明,函数的图象的变化问题,渗透了分类讨论,数形结合思想,是一道综合题.

练习册系列答案
相关题目
 设函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<
设函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|< 如图,A(
如图,A(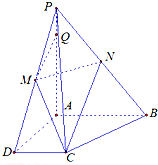 已知四棱锥P-ABCD中,PA⊥平面ABCD,且PA=4,底面为直角梯形,∠CDA=∠BAD=90°,AB=2,CD=1,AD=
已知四棱锥P-ABCD中,PA⊥平面ABCD,且PA=4,底面为直角梯形,∠CDA=∠BAD=90°,AB=2,CD=1,AD=