题目内容

已知定义域为R的函数f（x）=-2x+
a
2x+1
+2是奇函数，求a的值．
考点：指数函数综合题,函数奇偶性的性质
专题：函数的性质及应用
分析：根据：定义域为R的函数f（x）=-2x+
a
2x+1
+2是奇函数，得出f（0）=0，再代入解析式即可求解．
解答： 解：∵定义域为R的函数f（x）=-2x+
a
2x+1
+2是奇函数，
∴f（-x）=-f（x），f（0）=0，
∵f（x）=-2x+
a
2x+1
+2，
∴f（0）=20+
a
2
+2=0，1+2+
a
2
=0
∴a=-6，
点评：本题考查了奇函数的定义性质，属于容易题．
练习册系列答案
相关题目
已知函数f（x）=
a|x|-1
|x|
．
（1）写出函数f（x）的单调区间；
（2）若f（x）＜2x在（1，+∞）恒成立，求实数a的取值范围；
（3）若函数y=f（x）在[m，n]上值域是[m，n]（m≠n），求实数a的取值范围．
在平面直角坐标系xOy中，已知直线l的参数方程为
x=1-
2
2
t
y=2+
2
2
t
（t为参数），以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρsin2θ=4cosθ，直线l与曲线C交于A，B两点，则线段AB的长为
 
．
设A=a2+b2+5，B=2（2a-b），则A与B的大小关系为
 
．
若函数y=lg[（a2-1）x2+（a-1）x+1]的定义域为R，则实数a的取值范围是
 
．
在同一平面上射影长相等的两条斜线段的长度也相等
 
（判断对错）
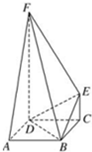如图，FD垂直于矩形ABCD所在平面，CE∥DF，∠DEF=90°．
（1）求证：BE∥平面ADF；
（2）若矩形ABCD的一边AB=
3
，EF=2
3
，则另一边BC的长为何值时，三棱锥F-BDE的体积为
3
．
求下列函数的值域：
（1）y=（
2
3
）-|x|；
（2）y=2
1
x-4
的值域．
已知{an}为等比数列，Sn为其前n项和，且an+1=2Sn+1（n≥1）；等差数列{bn}满足b4=a2，且9b2+a3=0，{bn}的前n项和为Tn．
（1）分别求an及Tn；
（2）是否存在k∈N*，使得Tk+ak∈（10，20），请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网