题目内容
 如图,从A到B有6条网线,数字表示该网线单位时间内可以通过的最大信息量,现从中任取3条网线且使每条网线通过最大信息量,设这三条网线通过的最大信息之和为ξ.
如图,从A到B有6条网线,数字表示该网线单位时间内可以通过的最大信息量,现从中任取3条网线且使每条网线通过最大信息量,设这三条网线通过的最大信息之和为ξ.(1)当ξ≥14时,线路信息畅通,求线路信息畅通的概率;
(2)求ξ的分布列和数学期望.
考点:离散型随机变量的期望与方差,等可能事件的概率,离散型随机变量及其分布列
专题:概率与统计
分析:(1)三条网线共有20种选择,其中ξ≥14的有5种,由此能求出结果;
(2)根据离散型随机变量的概率求法计算并列分布列即可.
(2)根据离散型随机变量的概率求法计算并列分布列即可.
解答:
解:(1)由题设知,三条网线共有20种选择,
其中ξ≥14的有5种,
∴线路信息畅通的概率P=
=
.
(2)由题设知ξ=10,11,12,13,14,15,
P(ξ=10)=
,
P(ξ=11)=
,
P(ξ=12)=
,
P(ξ=13)=
,
P(ξ=14)=
,
P(ξ=15)=
,
∴ξ的分布列:
Eξ=10×
+11×
+12×
+13×
+14×
+15×
=
.
其中ξ≥14的有5种,
∴线路信息畅通的概率P=
| 5 |
| 20 |
| 1 |
| 4 |
(2)由题设知ξ=10,11,12,13,14,15,
P(ξ=10)=
| 1 |
| 10 |
P(ξ=11)=
| 3 |
| 20 |
P(ξ=12)=
| 1 |
| 4 |
P(ξ=13)=
| 1 |
| 4 |
P(ξ=14)=
| 3 |
| 20 |
P(ξ=15)=
| 1 |
| 10 |
∴ξ的分布列:
| ξ=i | 10 | 11 | 12 | 13 | 14 | 15 | ||||||||||||
| P(ξ=i) |
|
|
|
|
|
|
| 1 |
| 10 |
| 3 |
| 20 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 20 |
| 1 |
| 10 |
| 25 |
| 2 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望,是中档题,是历年高考的必考题型之一.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
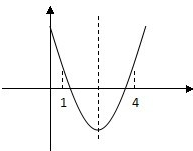 已知关于x不等式x2-2ax+a+2≤0(a∈R)的解集为M.
已知关于x不等式x2-2ax+a+2≤0(a∈R)的解集为M.