题目内容
5.已知方程x3+ax2+bx+c=0(a,b,c∈R).(1)设a=b=4,方程有三个不同实根,求c的取值范围;
(2)求证:a2-3b>0是方程有三个不同实根的必要不充分条件.
分析 (1)当a=b=4时,方程x3+4x2+4x+c=0有三个不同实根,等价于函数f(x)=x3+4x2+4x+c=0有三个不同零点,由f(x)的单调性知,当且仅当$c∈(0,\frac{32}{27})$时,函数f(x)=x3+4x2+4x+c有三个不同零点,可得结论;
(2)若函数f(x)有三个不同零点,则必有△=4a2-12b>0,故a2-3b>0是f(x)有三个不同零点的必要条件,再证明充分性即可.
解答 解:设f(x)=x3+ax2+bx+c.
(1)当a=b=4时,方程x3+4x2+4x+c=0有三个不同实根,等价于函数f(x)=x3+4x2+4x+c=0有三个不同零点,f'(x)=3x3+8x+4,令f'(x)=0得x1=-2或${x_2}=-\frac{2}{3}$,f(x)与f'(x)的区间(-∞,+∞)上情况如下:
| x | (-∞,-2) | -2 | (-2,-$\frac{2}{3}$) | -$\frac{2}{3}$ | (-$\frac{2}{3}$,+∞) |
| f(x) | + | 0 | - | 0 | + |
| f'(x) | c | c-$\frac{32}{27}$ |
使得f(x1)=f(x2)=f(x3)=0.
由f(x)的单调性知,当且仅当$c∈(0,\frac{32}{27})$时,函数f(x)=x3+4x2+4x+c有三个不同零点.
即方程x3+4x2+4x+c=0有三个不同实根.
(2)当△=4a2-12b<0时,f'(x)=3x2+2ax+b>0,x∈(-∞,+∞),
此时函数f(x)在区间(-∞,+∞)上单调递增,
所以f(x)不可能有三个不同零点.
当△=4a2-12b<0时,f'(x)=3x2+2ax+b只有一个零点,记作x0,
当x∈(-∞,x0)时,f'(x)>0,f(x)在区间(-∞,x0)上单调递增;
当x∈(x0,+∞)时,f'(x)>0,f(x)在区间(x0,+∞)上单调递增.
所以f(x)不可能有三个不同零点.
综上所述,若函数f(x)有三个不同零点,则必有△=4a2-12b>0.
故a2-3b>0是f(x)有三个不同零点的必要条件.
当a=b=4,c=0时,a2-3b>0,f(x)=x3+4x2+4x=x(x+2)2只有两个不同零点,
所以a2-3b>0不是f(x)有三个不同零点的充分条件.
因此a2-3b>0是f(x)有三个不同零点的必要而不充分条件.
即a2-3b>0是方程x3+ax2+bx+c=0有三个不同实根的必要而不充分条件.
点评 本题考查导数知识的综合运用,考查函数的单调性,考查函数的零点,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
13.已知函数f(x)的定义域是R,f(0)=2,对任意x∈R,f′(x)>f(x)+1,则下列正确的为( )
| A. | (f(1)+1)•e>f(2)+1 | B. | 3e<f(2)+1 | ||
| C. | 3•e≥f(1)+1 | D. | 3e2与f(2)+1大小不确定 |
20.下列命题中正确的是( )
| A. | 若p∨q为真命题,则p∧q为真命题 | |
| B. | “x=5”是“x2-4x-5=0”的充分不必要条件 | |
| C. | 命题“若x<-1,则x2-2x-3>0”的否命题为:“若x<-1,则x2-2x-3≤0” | |
| D. | 已知命题p:?x∈R,x2+x-1<0,则¬p:?x∈R,x2+x-1≥0 |
14.若函数f(x)为区间D上的凸函数,则对于D上的任意n个值x1、x2、…、xn,总有f(x1)+f(x2)+…+f(xn)≤nf($\frac{{x}_{1}+{x}_{2}+…+{x}_{n}}{n}$),现已知函数f(x)=sinx在[0,$\frac{π}{2}$]上是凸函数,则在锐角△ABC中,sinA+sinB+sinC的最大值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{3\sqrt{3}}{2}$ |
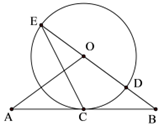 如图,直线AB经过⊙O上一点C,且OA=OB,CA=CB,⊙O交直线OB于E、D.
如图,直线AB经过⊙O上一点C,且OA=OB,CA=CB,⊙O交直线OB于E、D.