题目内容
5．假设你和同桌玩数字游戏，两人各自在心中想一个整数，分别记为x，y，且x，y∈[1，4]．如果满足|x-y|≤1，那么就称你和同桌“心灵感应”，则你和同桌“心灵感应”的概率为（ ）| A． | $\frac{7}{16}$ | B． | $\frac{5}{8}$ | C． | $\frac{9}{16}$ | D． | $\frac{7}{8}$ |
分析 两人所有的选数方法共有4×4=16 种，满足|x-y|≤1的方法数为 2×3+4=10，从而得到所求事件的概率．
解答 解：两人都从集合{1，2，3，4}中任选一个数写在纸上的方法总数为 4×4=16，
满足|x-y|≤1的方法数为 2×3+4=10．
故两人在一次游戏中“心灵感应”的概率为：
p=$\frac{10}{16}$=$\frac{5}{8}$，
故选：B．
点评 本题考查等可能事件的概率，求出满足|a-b|≤1的方法数为 2×3+4=10，是解题的关键．
练习册系列答案
相关题目
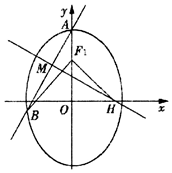已知椭圆C：$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1（{a＞b＞0}）$的上、下焦点分别为F1，F2，上焦点F1到直线 4x+3y+12=0的距离为3，椭圆C的离心率e=$\frac{1}{2}$．