题目内容
20.已知关于空间两条不同直线m,n,两个不同平面α,β,有下列四个命题:①若m∥α且n∥α,则m∥n;②若m⊥β且m⊥n,则n∥β;③若m⊥α且m∥β,则α⊥β;④若n?α且m不垂直于α,则m不垂直于n.其中正确命题的序号为③.分析 利用直线与平面的位置关系,通过反例判断命题的真假即可.
解答 解:空间两条不同直线m,n,两个不同平面α,β,
对于①若m∥α且n∥α,则m∥n;也可能相交,也可能异面,所以①不正确;
对于②若m⊥β且m⊥n,则n∥β;也可能n?β,所以②不正确;
对于③若m⊥α且m∥β,则α⊥β;由直线与平面垂直的性质可知③正确;
对于④若n?α且m不垂直于α,则m不垂直于n.错误,如果m∥α,但是平面α内有无数条直线与m垂直,特例例如正方体中的棱的位置关系.所以④不正确;
故答案为:③.
点评 本题考查命题的真假的判断与应用,空间直线与平面,直线与直线的位置关系的应用,是基础题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
8.设函数f(x)=$\left\{\begin{array}{l}{-|lnx|,x>0}\\{{x}^{2}+2x-1,x≤0}\end{array}\right.$,若f(a)=f(b)=f(c)=f(d),其中a,b,c,d互不相等,则对于命题p:abcd∈(0,1)和命题q:a+b+c+d∈[e+e-1-2,e2+e-2-2)真假的判断,正确的是( )
| A. | p假q真 | B. | p假q假 | C. | p真q真 | D. | p真q假 |
5.假设你和同桌玩数字游戏,两人各自在心中想一个整数,分别记为x,y,且x,y∈[1,4].如果满足|x-y|≤1,那么就称你和同桌“心灵感应”,则你和同桌“心灵感应”的概率为( )
| A. | $\frac{7}{16}$ | B. | $\frac{5}{8}$ | C. | $\frac{9}{16}$ | D. | $\frac{7}{8}$ |
12.设集合A={x|(x+4)(x-4)>0},B={x|-2<x≤6},则A∩B等于( )
| A. | (-2,4) | B. | (4,-2) | C. | (-4,6) | D. | (4,6] |
4.如图,某港口一天的水深变化曲线近似满足函数y=Asin$\frac{π}{6}$t+k,则水深从最小值变化到最大值至少需要( )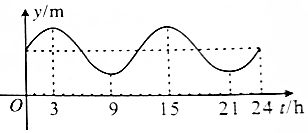

| A. | 6h | B. | 8h | C. | 12h | D. | 24h |
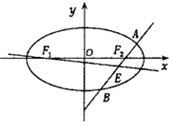 已知椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一条渐近线与x轴所成的夹角为30°,且双曲线的焦距为4$\sqrt{2}$.
已知椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一条渐近线与x轴所成的夹角为30°,且双曲线的焦距为4$\sqrt{2}$.