题目内容
15.把正数排列成如图甲的三角形数阵,然后擦去偶数行中的奇数和奇数行中的偶数,得到如图乙的三角形数阵,现把图乙中的数按从小到大的顺序排成一列,得到一个数列{an},若an=2017,则n=1031.
分析 观察乙图,发现第k行有k个数,第k行最后的一个数为k2,前k行共有$\frac{k(k+1)}{2}$个数,然后又因为442<2011<452,所以判断出这个数在第45行,而第45行的第一个数为1937,根据相邻两个数相差2,得到第45行38个数为2011,所以求出n即可
解答 解:图乙中第k行有k个数,第k行最后的一个数为k2,前k行共有$\frac{k(k+1)}{2}$个数,
由44×44=1936,45×45=2025知an=2011出现在第45行,第45行第一个数为1937,第$\frac{2017-1937}{2}+1$=41个数为2017,
所以n=$\frac{44(44+1)}{2}+41$=1031;
故答案为:1031;
点评 本题考查了归纳推理;考查学生会根据图形归纳总结规律来解决问题,会进行数列的递推式运算.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
6.已知函数f(x)=(x-t)|x|(t∈R),若存在t∈(0,2),对于任意x∈[-1,2],不等式f(x)>x+a都成立,则实数a的取值范围是( )
| A. | $a≤-\frac{1}{4}$ | B. | a≤0 | C. | $a≤\frac{1}{4}$ | D. | a≤2 |
7.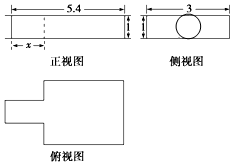 中国古代数学著作《九章算术》中记载了公元前344年商鞅督造一种标准量器--商鞅铜方升,一个爱好者根据该标准量器制作了一个几何体模型,该几何体的三视图如图所示(单位:寸),若几何体体积为13.5(立方寸),(π取3),则图中x的为( )
中国古代数学著作《九章算术》中记载了公元前344年商鞅督造一种标准量器--商鞅铜方升,一个爱好者根据该标准量器制作了一个几何体模型,该几何体的三视图如图所示(单位:寸),若几何体体积为13.5(立方寸),(π取3),则图中x的为( )
 中国古代数学著作《九章算术》中记载了公元前344年商鞅督造一种标准量器--商鞅铜方升,一个爱好者根据该标准量器制作了一个几何体模型,该几何体的三视图如图所示(单位:寸),若几何体体积为13.5(立方寸),(π取3),则图中x的为( )
中国古代数学著作《九章算术》中记载了公元前344年商鞅督造一种标准量器--商鞅铜方升,一个爱好者根据该标准量器制作了一个几何体模型,该几何体的三视图如图所示(单位:寸),若几何体体积为13.5(立方寸),(π取3),则图中x的为( )| A. | 2.4 | B. | 1.8 | C. | 1.6 | D. | 1.2 |
4.已知$cos(3π-α)=\frac{4}{5}$,则cos(π+α)的值是( )
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | -$\frac{3}{5}$ |
5.假设你和同桌玩数字游戏,两人各自在心中想一个整数,分别记为x,y,且x,y∈[1,4].如果满足|x-y|≤1,那么就称你和同桌“心灵感应”,则你和同桌“心灵感应”的概率为( )
| A. | $\frac{7}{16}$ | B. | $\frac{5}{8}$ | C. | $\frac{9}{16}$ | D. | $\frac{7}{8}$ |
