题目内容
13.已知正项数列{an}的首项a1=1,且(n+1)a${\;}_{n+1}^{2}$+anan+1-na${\;}_{n}^{2}$=0对?n∈N*都成立.(1)求{an}的通项公式;
(2)记bn=a2n-1a2n+1,数列{bn}的前n项和为Tn,证明:Tn<$\frac{1}{2}$.
分析 (1)(n+1)a${\;}_{n+1}^{2}$+anan+1-na${\;}_{n}^{2}$=0对?n∈N*都成立.分解因式可得:[(n+1)an+1-nan](an+1+an)=0,由an+1+an>0,可得(n+1)an+1-nan=0,即$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{n}{n+1}$.利用“累乘求积”方法即可得出.
(2)bn=a2n-1a2n+1=$\frac{1}{2n-1}•\frac{1}{2n+1}$=$\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$.利用裂项求和方法、数列的单调性即可得出.
解答 (1)解:(n+1)a${\;}_{n+1}^{2}$+anan+1-na${\;}_{n}^{2}$=0对?n∈N*都成立.
∴[(n+1)an+1-nan](an+1+an)=0,∵an+1+an>0,
∴(n+1)an+1-nan=0,即$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{n}{n+1}$.
∴an=$\frac{{a}_{n}}{{a}_{n-1}}•\frac{{a}_{n-1}}{{a}_{n-2}}$•…•$\frac{{a}_{2}}{{a}_{1}}•{a}_{1}$=$\frac{n-1}{n}•\frac{n-2}{n-1}$•…•$\frac{1}{2}$•1=$\frac{1}{n}$.
(2)证明:bn=a2n-1a2n+1=$\frac{1}{2n-1}•\frac{1}{2n+1}$=$\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$.
数列{bn}的前n项和为Tn=$\frac{1}{2}[(1-\frac{1}{3})+(\frac{1}{3}-\frac{1}{5})$+…+$(\frac{1}{2n-1}-\frac{1}{2n+1})]$
=$\frac{1}{2}(1-\frac{1}{2n+1})$$<\frac{1}{2}$.
即Tn<$\frac{1}{2}$.
点评 本题考查了数列递推关系、“累乘求积”方法、裂项求和方法、数列的单调性,考查了推理能力与计算能力,属于中档题.

| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | -$\frac{3}{5}$ |
| A. | 1 | B. | 2 | C. | 2$\sqrt{2}$ | D. | 3 |
| A. | p假q真 | B. | p假q假 | C. | p真q真 | D. | p真q假 |
| A. | $\frac{7}{16}$ | B. | $\frac{5}{8}$ | C. | $\frac{9}{16}$ | D. | $\frac{7}{8}$ |
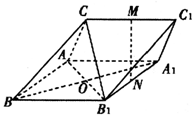 如图,三棱柱ABC-A1B1Cl中,M,N分别为CC1,A1B1的中点.CA⊥CB1,CA=CB1,BA=BC=BB1.
如图,三棱柱ABC-A1B1Cl中,M,N分别为CC1,A1B1的中点.CA⊥CB1,CA=CB1,BA=BC=BB1.