Question

18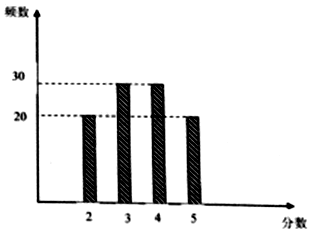．某校后勤处为跟踪调查该校餐厅的当月的服务质量，兑现奖惩，从就餐的学生中随机抽出100位学生对餐厅服务质量打分（5分制），得到如图柱状图．
（Ⅰ）从样本中任意选取2名学生，求恰好有1名学生的打分不低于4分的概率；
（Ⅱ）若以这100人打分的频率作为概率，在该校随机选取2名学生进行打分（学生打分之间相互独立）记X表示两人打分之和，求X的分布列和E（X）．
（Ⅲ）根据（Ⅱ）的计算结果，后勤处对餐厅服务质量情况定为三个等级，并制定了对餐厅相应的奖惩方案，如表所示，设当月奖金为Y（单位：元），求E（Y）．

服务质量评分X	X≤5	6≤X≤8	X≥9
等级	不好	较好	优良
奖惩标准（元）	-1000	2000	3000

Answer 1

分析 （Ⅰ）计算“从样本中任意选取2名学生，恰好有一名学生的打分不低于4分”的概率值；
（Ⅱ）由X的可能取值，计算对应的概率值，写出X的分布列，计算数学期望；
（Ⅲ）根据表格写出Y的分布列，计算对应的数学期望值．

解答 解：（Ⅰ）设“从样本中任意选取2名学生，求恰好有一名学生的打分不低于4分”为事件A，
则P（A）=$\frac{{C}_{50}^{1}{•C}_{50}^{1}}{{C}_{100}^{2}}$=$\frac{50}{99}$≈0.51；…（3分）
（Ⅱ）X的可能取值为4，5，6，7，8，9，10；
则P（X=4）=0.2×0.2=0.04，
P（X=5）=2×0.2×0.3=0.12，
P（X=6）=2×0.2×0.3+0.3×0.3=0.21，
P（X=7）=2×0.3×0.3+2×0.2×0.2=0.26，
P（X=8）=2×0.2×0.3+0.3×0.3=0.21，
P（X=9）=2×0.2×0.3=0.12，
P（X=10）=0.2×0.2=0.04；
X的分布列如下：

X	4	5	6	7	8	9	10
P	0.04	0.12	0.21	0.26	0.21	0.12	0.04

X的数学期望为E（X）=4×0.04+5×0.12+6×0.21+7×0.26+8×0.21+9×0.12+10×0.04=7；…..（9分）
（Ⅲ）Y的分布列为

Y	-1000	2000	3000
P	0.16	0.68	0.16

Y的数学期望为E（Y）=-1000×0.16+2000×0.68+3000×0.16=1680．…（12分）

点评 本题考查了频率分布直方图与离散型随机变量的分布列和数学期望的计算问题，是综合性题目．