题目内容
13．设{an}是公差为2的等差数列，bn=a${\;}_{{2}^{n}}$，若{bn}为等比数列，则b1+b2+b3+b4+b5=（ ）| A． | 142 | B． | 124 | C． | 128 | D． | 144 |
分析 由已知得an=a1+（n-1）×2=a1+2n-2，且（a4）2=a2•a8，从而a1=2，${b}_{n}={a}_{{2}^{n}}$=2+2×2n-2=2n+1，由此能求出b1+b2+b3+b4+b5的值．
解答 解：∵{an}是公差为2的等差数列，bn=a${\;}_{{2}^{n}}$，
∴an=a1+（n-1）×2=a1+2n-2，
∵{bn}为等比数列，
∴${{b}_{2}}^{2}={b}_{1}{b}_{3}$．∴（a4）2=a2•a8，
∴$（{a}_{1}+8-2）^{2}$=（a1+4-2）（a1+16-2），
解得a1=2，
∴${b}_{n}={a}_{{2}^{n}}$=2+2×2n-2=2n+1
b1+b2+b3+b4+b5=22+23+24+25+26=124．
故选：B．
点评 本题考查等比数列的前5项和的求法，是基础题，解题时要认真审题，注意等差数列、等比数列的性质的合理运用．
练习册系列答案
相关题目
4．设△ABC的内角A，B，C分别对应边a，b，c．若c2=（a-b）2+6，${S_{△ABC}}=\frac{3}{2}\sqrt{3}$，则角C=（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{π}{6}$ | C． | $\frac{3}{4}π$ | D． | $\frac{2}{3}π$ |
1．已知函数f（x）是定义在R上的奇函数，其导函数为f′（x），若对任意实数x都有x2f′（x）＞2xf（-x），则不等式x2f（x）＜（3x-1）2f（1-3x）的解集是（ ）
| A． | （$\frac{1}{4}$，+∞） | B． | （0，$\frac{1}{4}$） | C． | （-∞，$\frac{1}{4}$） | D． | （-∞，$\frac{1}{4}$）∪（$\frac{1}{4}$，+∞） |
18．
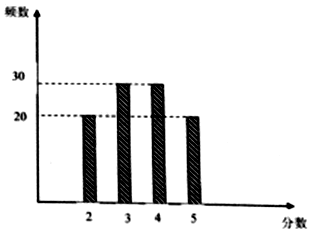某校后勤处为跟踪调查该校餐厅的当月的服务质量，兑现奖惩，从就餐的学生中随机抽出100位学生对餐厅服务质量打分（5分制），得到如图柱状图．
（Ⅰ）从样本中任意选取2名学生，求恰好有1名学生的打分不低于4分的概率；
（Ⅱ）若以这100人打分的频率作为概率，在该校随机选取2名学生进行打分（学生打分之间相互独立）记X表示两人打分之和，求X的分布列和E（X）．
（Ⅲ）根据（Ⅱ）的计算结果，后勤处对餐厅服务质量情况定为三个等级，并制定了对餐厅相应的奖惩方案，如表所示，设当月奖金为Y（单位：元），求E（Y）．
某校后勤处为跟踪调查该校餐厅的当月的服务质量，兑现奖惩，从就餐的学生中随机抽出100位学生对餐厅服务质量打分（5分制），得到如图柱状图．（Ⅰ）从样本中任意选取2名学生，求恰好有1名学生的打分不低于4分的概率；
（Ⅱ）若以这100人打分的频率作为概率，在该校随机选取2名学生进行打分（学生打分之间相互独立）记X表示两人打分之和，求X的分布列和E（X）．
（Ⅲ）根据（Ⅱ）的计算结果，后勤处对餐厅服务质量情况定为三个等级，并制定了对餐厅相应的奖惩方案，如表所示，设当月奖金为Y（单位：元），求E（Y）．
| 服务质量评分X | X≤5 | 6≤X≤8 | X≥9 |
| 等级 | 不好 | 较好 | 优良 |
| 奖惩标准（元） | -1000 | 2000 | 3000 |
5．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）上一点到两个焦点的距离分别为10和4，且离心率为2，则该双曲线的虚轴长为（ ）
| A． | 3 | B． | 6 | C． | 3$\sqrt{3}$ | D． | 6$\sqrt{3}$ |
3．已知抛物线y2=4x，过焦点F作直线与抛物线交于点A，B，设|AF|=m，|BF|=n，则m+n的最小值为（ ）
| A． | 2 | B． | 3 | C． | $\sqrt{3}$ | D． | 4 |