��Ŀ����
9����A��B�ֱ���ֱ��$y=\frac{{\sqrt{2}}}{2}x$��$y=-\frac{{\sqrt{2}}}{2}x$�ϵĶ��㣬��$|AB|=2\sqrt{2}$����OΪ����ԭ�㣬����P����$\overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{OB}$������ ��P�Ĺ켣����C1��
����һֱ˫����C2��C1���϶���Ϊ���㣬��һ�������߷���Ϊx+2y=0����˫����C2�ķ��̣�
���� ���� ��$A��{x_1}��\frac{{\sqrt{2}}}{2}{x_1}����B��{x_2}��-\frac{{\sqrt{2}}}{2}{x_2}��$����$|AB|=2\sqrt{2}$���ã�x1-x2��2+$\frac{1}{2}$��x1+x2��2=8������P��x��y������$\overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{OB}$����$\left\{\begin{array}{l}x={x_1}+{x_2}\\ y=\frac{{\sqrt{2}}}{2}��{x_1}-{x_2}��\end{array}\right.$�����Т������ö���P�Ĺ켣����C1
������˫���߷���Ϊ$\frac{y^2}{m^2}-\frac{x^2}{n^2}=1$���ɣ���֪����Բ�϶��㣨0��2��������m2+n2=4����m+2n=0��${m^2}=\frac{4}{5}$��${n^2}=\frac{16}{5}$���ɣ�
��� �⣺���� ��$A��{x_1}��\frac{{\sqrt{2}}}{2}{x_1}����B��{x_2}��-\frac{{\sqrt{2}}}{2}{x_2}��$��
��$|AB|=2\sqrt{2}$���ࣨx1-x2��2+$\frac{1}{2}$��x1+x2��2=8����
��P��x��y������$\overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{OB}$����$\left\{\begin{array}{l}x={x_1}+{x_2}\\ y=\frac{{\sqrt{2}}}{2}��{x_1}-{x_2}��\end{array}\right.$
�����Т������ã�$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{4}=1$��
����P�Ĺ켣����C1��$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{4}=1$��
������˫���߷���Ϊ$\frac{y^2}{m^2}-\frac{x^2}{n^2}=1$��
�ɣ���֪����Բ�϶��㣨0��2����
����m2+n2=4����x+2y=0��$y=\frac{1}{2}x$����$\frac{m}{n}=\frac{1}{2}$��
���${m^2}=\frac{4}{5}$��${n^2}=\frac{16}{5}$
���ԣ�˫���߷���Ϊ$\frac{{5{y^2}}}{4}-\frac{{5{x^2}}}{16}=1$��
���� ���⿼������ص㷨��켣���̣�����֪˫���߽�������˫���߷��̵ķ����������е��⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | $\sqrt{2}$ | B�� | $\sqrt{3}$ | C�� | 2 | D�� | $\sqrt{5}$ |
| A�� | $\frac{��}{3}$ | B�� | $\frac{��}{6}$ | C�� | $\frac{3}{4}��$ | D�� | $\frac{2}{3}��$ |
| A�� | $\overrightarrow{a}$+$\overrightarrow{b}$ | B�� | $\overrightarrow{a}$-$\overrightarrow{b}$ | C�� | 2$\overrightarrow{a}$-$\overrightarrow{b}$ | D�� | $\overrightarrow{a}$-2$\overrightarrow{b}$ |
| A�� | ��$\frac{1}{4}$��+�ޣ� | B�� | ��0��$\frac{1}{4}$�� | C�� | ��-�ޣ�$\frac{1}{4}$�� | D�� | ��-�ޣ�$\frac{1}{4}$���ȣ�$\frac{1}{4}$��+�ޣ� |
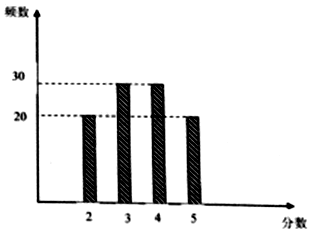 ijУ���ڴ�Ϊ���ٵ����У�����ĵ��µķ������������ֽ��ͣ��ӾͲ͵�ѧ����������100λѧ���Բ�������������֣�5���ƣ����õ���ͼ��״ͼ��
ijУ���ڴ�Ϊ���ٵ����У�����ĵ��µķ������������ֽ��ͣ��ӾͲ͵�ѧ����������100λѧ���Բ�������������֣�5���ƣ����õ���ͼ��״ͼ����������������ѡȡ2��ѧ������ǡ����1��ѧ���Ĵ�ֲ�����4�ֵĸ��ʣ�
����������100�˴�ֵ�Ƶ����Ϊ���ʣ��ڸ�У���ѡȡ2��ѧ�����д�֣�ѧ�����֮�����������X��ʾ���˴��֮�ͣ���X�ķֲ��к�E��X����
�����ݣ��ļ����������ڴ��Բ����������������Ϊ�����ȼ������ƶ��˶Բ�����Ӧ�Ľ��ͷ����������ʾ���赱�½���ΪY����λ��Ԫ������E��Y����
| ������������X | X��5 | 6��X��8 | X��9 |
| �ȼ� | ���� | �Ϻ� | ���� |
| ���ͱ���Ԫ�� | -1000 | 2000 | 3000 |