题目内容
10.已知f(x)=2$\sqrt{3}$sinxcos-cos(π+2x).(Ⅰ)求f(x)的单调增区间;
(Ⅱ)在△ABC中,角A,B,C的对边分别是a,b,c,若f(C)=1,c=$\sqrt{3}$,a+b=2$\sqrt{3}$,求△ABC的面积.
分析 (1)利用二倍角和诱导公式以及辅助角公式基本公式将函数化为y=Asin(ωx+φ)的形式,将内层函数看作整体,放到正弦函数的增区间上,解不等式得函数的单调递增区间;
(2)根据f(C)=1,求出角C的大小,c=$\sqrt{3}$,a+b=2$\sqrt{3}$,利用余弦定理建立关系,可求△ABC的面积.
解答 解:(1)f(x)=2$\sqrt{3}$sinxcos-cos(π+2x).
化简可得:f(x)$\sqrt{3}$sin2x+cos2x=2sin(2x+$\frac{π}{6}$)
由$-\frac{π}{2}+2kπ≤2x+\frac{π}{6}≤\frac{π}{2}+2kπ$得:$-\frac{π}{3}+kπ$≤x≤$\frac{π}{6}+kπ$.
∴f(x)的单调增区间为[$-\frac{π}{3}+kπ$,$\frac{π}{6}+kπ$],k∈Z.
(2)由(1)可知f(x)=2sin(2x+$\frac{π}{6}$)
∵f(C)=1,即2sin(2C+$\frac{π}{6}$)=1,
∵0<C<π
可得:2C+$\frac{π}{6}$=$\frac{5π}{6}$
∴C=$\frac{π}{3}$.
由a+b=2$\sqrt{3}$,可得a2+b2=12-2ab.
∵c=$\sqrt{3}$,
根据余弦定理:cosC=$\frac{a^2+b^2-{c}^{2}}{2ab}$可得:$\frac{12-2ab-{c}^{2}}{2ab}=\frac{1}{2}$,
解得:ab=3.
故得△ABC的面积$S=\frac{1}{2}absinC=\frac{1}{2}×3×\frac{\sqrt{3}}{2}=\frac{3\sqrt{3}}{4}$.
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,利用三角函数公式将函数进行化简是解决本题的关键.同时考查了余弦定理的运用和△ABC的面积的公式.属于中档题.

 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案| A. | ($\frac{1}{4}$,+∞) | B. | (0,$\frac{1}{4}$) | C. | (-∞,$\frac{1}{4}$) | D. | (-∞,$\frac{1}{4}$)∪($\frac{1}{4}$,+∞) |
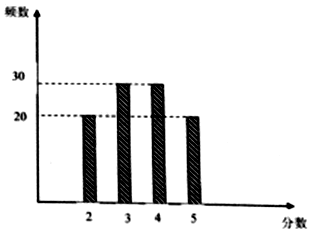 某校后勤处为跟踪调查该校餐厅的当月的服务质量,兑现奖惩,从就餐的学生中随机抽出100位学生对餐厅服务质量打分(5分制),得到如图柱状图.
某校后勤处为跟踪调查该校餐厅的当月的服务质量,兑现奖惩,从就餐的学生中随机抽出100位学生对餐厅服务质量打分(5分制),得到如图柱状图.(Ⅰ)从样本中任意选取2名学生,求恰好有1名学生的打分不低于4分的概率;
(Ⅱ)若以这100人打分的频率作为概率,在该校随机选取2名学生进行打分(学生打分之间相互独立)记X表示两人打分之和,求X的分布列和E(X).
(Ⅲ)根据(Ⅱ)的计算结果,后勤处对餐厅服务质量情况定为三个等级,并制定了对餐厅相应的奖惩方案,如表所示,设当月奖金为Y(单位:元),求E(Y).
| 服务质量评分X | X≤5 | 6≤X≤8 | X≥9 |
| 等级 | 不好 | 较好 | 优良 |
| 奖惩标准(元) | -1000 | 2000 | 3000 |
| A. | 3 | B. | 6 | C. | 3$\sqrt{3}$ | D. | 6$\sqrt{3}$ |
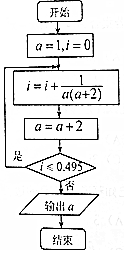 已知某程序框图如图所示,则执行该程序后输出的结果是( )
已知某程序框图如图所示,则执行该程序后输出的结果是( )| A. | 98 | B. | 99 | C. | 100 | D. | 101 |