题目内容
6. 已知椭圆C;$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>c)的左、右焦点分别为F1(-c,0)、F2(c,0),过原点O的直线(与x轴不重合)与椭圆C相交于D、Q两点,且|DF1|+|QF1|=4,P为椭圆C上的动点,△PF1F2的面积的最大值为$\sqrt{3}$.
已知椭圆C;$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>c)的左、右焦点分别为F1(-c,0)、F2(c,0),过原点O的直线(与x轴不重合)与椭圆C相交于D、Q两点,且|DF1|+|QF1|=4,P为椭圆C上的动点,△PF1F2的面积的最大值为$\sqrt{3}$.(1)求椭圆C的离心率;
(2)若过左焦点F1的任意直线与椭圆C相交于S、T两点,求$\overrightarrow{OS}$$•\overrightarrow{OT}$的取值范围.
分析 (1)由题意可得a,再由,△PF1F2的面积的最大值为$\sqrt{3}$得到bc=$\sqrt{3}$,结合隐含条件求得b,c的值,则椭圆离心率可求;
(2)由(1)求出椭圆方程,当直线ST的斜率不存在时,求出S,T的坐标,可得$\overrightarrow{OS}$$•\overrightarrow{OT}$的值;当直线ST的斜率存在时,设直线ST的方程为y=m(x+1),将直线ST的方程y=m(x+1)代入椭圆方程,化为关于x的一元二次方程,利用根与系数的关系结合向量数量积的坐标运算求得$\overrightarrow{OS}$$•\overrightarrow{OT}$的取值范围.
解答 解:(1)由题意可知,2a=4,a=2.
又bc=$\sqrt{3}$,且b2+c2=4,解得b=$\sqrt{3}$,c=1.
∴椭圆的离心率e=$\frac{c}{a}=\frac{1}{2}$;
(2)由(1)得椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.
当直线ST的斜率不存在时,有S(-1,$\frac{3}{2}$)、T(-1,$-\frac{3}{2}$),
此时$\overrightarrow{OS}•\overrightarrow{OT}=-\frac{5}{4}$.
当直线ST的斜率存在时,设直线ST的方程为y=m(x+1),
再设点S(x1,y1),T(x2,y2),
将直线ST的方程y=m(x+1)代入椭圆方程消去y并整理得:
(4m2+3)x2+8m2x+4m2-12=0.
得${x}_{1}+{x}_{2}=\frac{-8{m}^{2}}{4{m}^{2}+3}$,${x}_{1}{x}_{2}=\frac{4{m}^{2}-12}{4{m}^{2}+3}$.
从而$\overrightarrow{OS}•\overrightarrow{OT}={x}_{1}{x}_{2}+{y}_{1}{y}_{2}={x}_{1}{x}_{2}+{m}^{2}({x}_{1}+1)({x}_{2}+1)$
=$({m}^{2}+1){x}_{1}{x}_{2}+{m}^{2}({x}_{1}+{x}_{2})+{m}^{2}$=$\frac{({m}^{2}+1)(4{m}^{2}-12)}{4{m}^{2}+3}+\frac{-8{m}^{4}}{4{m}^{2}+3}+\frac{4{m}^{4}+3{m}^{2}}{4{m}^{2}+3}$
=$\frac{-5{m}^{2}-12}{4{m}^{2}+3}$=$-4+\frac{11{m}^{2}}{4{m}^{2}+3}=-\frac{5}{4}-\frac{33}{4{m}^{2}+3}$∈[-4,-$\frac{5}{4}$).
综上所述,$\overrightarrow{OS}$$•\overrightarrow{OT}$的取值范围为[-4,-$\frac{5}{4}$].
点评 本题考查椭圆的简单性质,考查了直线与椭圆位置关系的应用,训练了平面向量在求解圆锥曲线问题中的应用,是中档题.

| A. | y=±$\sqrt{2}x$ | B. | y=±$\frac{\sqrt{2}}{2}$x | C. | y=±2x | D. | y=±$\frac{1}{2}$x |
| A. | $\overrightarrow{a}$+$\overrightarrow{b}$ | B. | $\overrightarrow{a}$-$\overrightarrow{b}$ | C. | 2$\overrightarrow{a}$-$\overrightarrow{b}$ | D. | $\overrightarrow{a}$-2$\overrightarrow{b}$ |
| A. | ($\frac{1}{4}$,+∞) | B. | (0,$\frac{1}{4}$) | C. | (-∞,$\frac{1}{4}$) | D. | (-∞,$\frac{1}{4}$)∪($\frac{1}{4}$,+∞) |

| A. | 8 | B. | 13 | C. | 21 | D. | 34 |
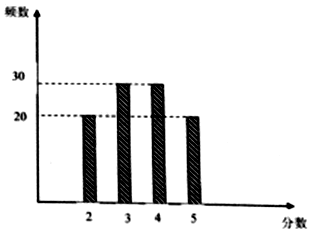 某校后勤处为跟踪调查该校餐厅的当月的服务质量,兑现奖惩,从就餐的学生中随机抽出100位学生对餐厅服务质量打分(5分制),得到如图柱状图.
某校后勤处为跟踪调查该校餐厅的当月的服务质量,兑现奖惩,从就餐的学生中随机抽出100位学生对餐厅服务质量打分(5分制),得到如图柱状图.(Ⅰ)从样本中任意选取2名学生,求恰好有1名学生的打分不低于4分的概率;
(Ⅱ)若以这100人打分的频率作为概率,在该校随机选取2名学生进行打分(学生打分之间相互独立)记X表示两人打分之和,求X的分布列和E(X).
(Ⅲ)根据(Ⅱ)的计算结果,后勤处对餐厅服务质量情况定为三个等级,并制定了对餐厅相应的奖惩方案,如表所示,设当月奖金为Y(单位:元),求E(Y).
| 服务质量评分X | X≤5 | 6≤X≤8 | X≥9 |
| 等级 | 不好 | 较好 | 优良 |
| 奖惩标准(元) | -1000 | 2000 | 3000 |
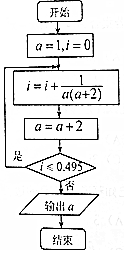 已知某程序框图如图所示,则执行该程序后输出的结果是( )
已知某程序框图如图所示,则执行该程序后输出的结果是( )| A. | 98 | B. | 99 | C. | 100 | D. | 101 |

| A. | i≥10? | B. | i<10? | C. | i≥11? | D. | i<11? |