题目内容
3．已知x∈R，则“x＞2”是“x2-3x+2＞0”成立的（ ）| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
分析 根据不等式的关系，结合充分条件和必要条件的定义进行判断即可．
解答 解：由x2-3x+2＞0得x＞2或x＜-1，
则“x＞2”是“x2-3x+2＞0”成立的充分不必要条件，
故选：A
点评 本题主要考查充分条件和必要条件的判断，比较基础．
练习册系列答案
相关题目
14．已知向量$\overrightarrow{a}$=（1，0），$\overrightarrow{b}$=（0，1），则下列向量中与向量2$\overrightarrow{a}$+$\overrightarrow{b}$垂直的是（ ）
| A． | $\overrightarrow{a}$+$\overrightarrow{b}$ | B． | $\overrightarrow{a}$-$\overrightarrow{b}$ | C． | 2$\overrightarrow{a}$-$\overrightarrow{b}$ | D． | $\overrightarrow{a}$-2$\overrightarrow{b}$ |
11．执行如图所示的程序框图，则输出的结果是（ ）
| A． | 8 | B． | 13 | C． | 21 | D． | 34 |
18．
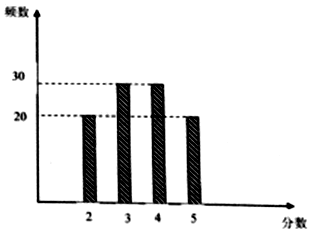某校后勤处为跟踪调查该校餐厅的当月的服务质量，兑现奖惩，从就餐的学生中随机抽出100位学生对餐厅服务质量打分（5分制），得到如图柱状图．
（Ⅰ）从样本中任意选取2名学生，求恰好有1名学生的打分不低于4分的概率；
（Ⅱ）若以这100人打分的频率作为概率，在该校随机选取2名学生进行打分（学生打分之间相互独立）记X表示两人打分之和，求X的分布列和E（X）．
（Ⅲ）根据（Ⅱ）的计算结果，后勤处对餐厅服务质量情况定为三个等级，并制定了对餐厅相应的奖惩方案，如表所示，设当月奖金为Y（单位：元），求E（Y）．
某校后勤处为跟踪调查该校餐厅的当月的服务质量，兑现奖惩，从就餐的学生中随机抽出100位学生对餐厅服务质量打分（5分制），得到如图柱状图．（Ⅰ）从样本中任意选取2名学生，求恰好有1名学生的打分不低于4分的概率；
（Ⅱ）若以这100人打分的频率作为概率，在该校随机选取2名学生进行打分（学生打分之间相互独立）记X表示两人打分之和，求X的分布列和E（X）．
（Ⅲ）根据（Ⅱ）的计算结果，后勤处对餐厅服务质量情况定为三个等级，并制定了对餐厅相应的奖惩方案，如表所示，设当月奖金为Y（单位：元），求E（Y）．
| 服务质量评分X | X≤5 | 6≤X≤8 | X≥9 |
| 等级 | 不好 | 较好 | 优良 |
| 奖惩标准（元） | -1000 | 2000 | 3000 |
15．
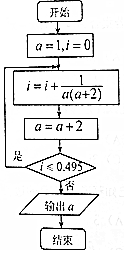已知某程序框图如图所示，则执行该程序后输出的结果是（ ）
已知某程序框图如图所示，则执行该程序后输出的结果是（ ）| A． | 98 | B． | 99 | C． | 100 | D． | 101 |