题目内容
已知椭圆
+
=1的弦AB的中点M的坐标为(2,1),求直线AB的方程,并求AB的长.
| x2 |
| 16 |
| y2 |
| 4 |
考点:直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:首先,根据椭圆的对称轴,得到该直线的斜率存在,设其方程为y-1=k(x-2),然后联立方程组,利用一元二次方程根与系数的关系,并且借助于中点坐标公式,确定斜率k的值,然后,利用两点间的距离公式或弦长公式,求解AB的长.
解答:
解:当直线AB的斜率不存在时,不成立,
故直线AB的斜率存在,
设其方程为y-1=k(x-2),
联立方程组
,消去y并整理,得
(1+4k2)x2+8k(1-2k)x+4(1-2k)2-16=0,
∴x1+x2=-
,
∵
=2,
∴2k(2k-1)=1+4k2,
∴k=-
,
∴直线AB的方程:x+2y-4=0.
将k=-
代人(1+4k2)x2+8k(1-2k)x+4(1-2k)2-16=0,
得x2-4x=0,
解得x=0,x=4,
∴A(0,
),B(4,-
),
∴|AB|=
=2
.
∴AB的长2
.
故直线AB的斜率存在,
设其方程为y-1=k(x-2),
联立方程组
|
(1+4k2)x2+8k(1-2k)x+4(1-2k)2-16=0,
∴x1+x2=-
| 8k(1-2k) |
| 1+4k2 |
∵
| x1+x2 |
| 2 |
∴2k(2k-1)=1+4k2,
∴k=-
| 1 |
| 2 |
∴直线AB的方程:x+2y-4=0.
将k=-
| 1 |
| 2 |
得x2-4x=0,
解得x=0,x=4,
∴A(0,
| 3 |
| 2 |
| 1 |
| 2 |
∴|AB|=
42+(-
|
| 5 |
∴AB的长2
| 5 |
点评:本题属于中档题,重点考查了椭圆的简单几何性质、直线与椭圆的位置关系、弦长公式、两点间的距离公式等知识,属于高考的热点和重点问题.

练习册系列答案
 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
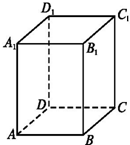 如图,已知长方体ABCD-A1B1C1D1中,AB=
如图,已知长方体ABCD-A1B1C1D1中,AB=