题目内容
13.在梯形ABCD中,$\overrightarrow{AB}$=3$\overrightarrow{DC}$,则$\overrightarrow{BC}$等于( )| A. | -$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AD}$ | B. | -$\frac{2}{3}$$\overrightarrow{AB}$+$\frac{4}{3}$$\overrightarrow{AD}$ | C. | $\frac{2}{3}$$\overrightarrow{AB}$+$\overrightarrow{AD}$ | D. | -$\frac{2}{3}$$\overrightarrow{AB}$+$\overrightarrow{AD}$ |
分析 在梯形ABCD中,过C作CE∥AD,交AB与E,又$\overrightarrow{AB}$=3$\overrightarrow{DC}$,则$\overrightarrow{BC}$=$\overrightarrow{BE}+\overrightarrow{EC}$=$\frac{2}{3}\overrightarrow{BA}+\overrightarrow{AD}$=$-\frac{2}{3}\overrightarrow{AB}+\overrightarrow{AD}$
解答  解:在梯形ABCD中,过C作CE∥AD,交AB与E,又$\overrightarrow{AB}$=3$\overrightarrow{DC}$,
解:在梯形ABCD中,过C作CE∥AD,交AB与E,又$\overrightarrow{AB}$=3$\overrightarrow{DC}$,
则$\overrightarrow{BC}$=$\overrightarrow{BE}+\overrightarrow{EC}$=$\frac{2}{3}\overrightarrow{BA}+\overrightarrow{AD}$=$-\frac{2}{3}\overrightarrow{AB}+\overrightarrow{AD}$;
故选:D
点评 本题考查了向量的线性运算,属于基础题.

练习册系列答案
相关题目
3.若将θ视为变量,则以原点为圆心,r为半径的圆可表示为$\left\{\begin{array}{l}{x=rcosθ}\\{y=rsinθ}\end{array}\right.$(θ∈[0,2π)),问下列何种表示可表示以(a,b)为圆心,r为半径的圆( )
| A. | $\left\{\begin{array}{l}{x=rcosθ-a}\\{y=rsinθ-b}\end{array}\right.$(θ∈[0,2π)) | B. | $\left\{\begin{array}{l}{x=rcosθ+a}\\{y=rsinθ+b}\end{array}\right.$(θ∈[0,2π)) | ||
| C. | $\left\{\begin{array}{l}{x=-rcosθ-a}\\{y=-rsinθ-b}\end{array}\right.$(θ∈[0,2π)) | D. | $\left\{\begin{array}{l}{x=rsinθ-a}\\{y=rcosθ-b}\end{array}\right.$(θ∈[0,2π)) |
1.若直线1:ax+by+1=0(a>0,b>0)把圆C:(x+4)2+(y+1)2=16分成面积相等的两部分,则当ab取得最大值时,坐标原点到直线1的距离是( )
| A. | 4 | B. | 8$\sqrt{17}$ | C. | 2 | D. | $\frac{8\sqrt{17}}{17}$ |
18.设随机变量X服从正态分布N(4,σ2),若P(X>m)=0.3,则P(X>8-m)=( )
| A. | 0.2 | B. | 0.3 | C. | 0.7 | D. | 与σ的值有关 |
5.某几何体的三视图如图所示,则其体积为( )
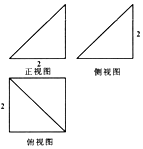

| A. | 4 | B. | 8 | C. | $\frac{4}{3}$ | D. | $\frac{8}{3}$ |
2.下列结论为真的个数是( )
(1)“x2+2x-3<0”是命题
(2)命题“若p,则q”的否命题是“若p,则¬q”
(3)当q是p的必要条件时,p是q的充分条件
(4)“若p不成立,则q不成立”等价于“若q成立,则p成立”
(1)“x2+2x-3<0”是命题
(2)命题“若p,则q”的否命题是“若p,则¬q”
(3)当q是p的必要条件时,p是q的充分条件
(4)“若p不成立,则q不成立”等价于“若q成立,则p成立”
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.分析法证明命题中所说的“执果索因”是指寻求使命题成立的( )
| A. | 必要条件 | B. | 充分条件 | C. | 充要条件 | D. | 必要或充分条件 |