题目内容
3．分析法证明命题中所说的“执果索因”是指寻求使命题成立的（ ）| A． | 必要条件 | B． | 充分条件 | C． | 充要条件 | D． | 必要或充分条件 |
分析 利用分析法证明不等式的方法和步骤，结合充分条件的定义，做出判断．
解答 解：用分析法证明不等式成立时用的方法是：要证此不等式成立，只要证明某条件具备即可，也就是说只要某条件具备，
此不等式就一定成立，故某条件具备是不等式成立的充分条件．因此，“执果索因”是指寻求使不等式成立的充分条件，
故选 B．
点评 本题考查用分析法证明不等式的方法，充分条件的定义．
练习册系列答案
名校课堂系列答案
相关题目
13．在梯形ABCD中，$\overrightarrow{AB}$=3$\overrightarrow{DC}$，则$\overrightarrow{BC}$等于（ ）
| A． | -$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AD}$ | B． | -$\frac{2}{3}$$\overrightarrow{AB}$+$\frac{4}{3}$$\overrightarrow{AD}$ | C． | $\frac{2}{3}$$\overrightarrow{AB}$+$\overrightarrow{AD}$ | D． | -$\frac{2}{3}$$\overrightarrow{AB}$+$\overrightarrow{AD}$ |
14．已知点A（-1，2），B（2，3），若直线l：kx-y-k+1=0与线段AB相交，则实数k的取值范围是（ ）
| A． | （-∞，-$\frac{1}{2}$]∪[2，+∞） | B． | [{-$\frac{1}{2}$，2}] | C． | [-2，$\frac{1}{2}$] | D． | （-∞，-2]∪[$\frac{1}{2}$，+∞） |
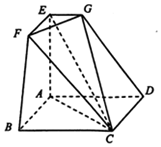如图所示的空间几何体ABCDEFG中，四边形ABCD是边长为2的正方形，AE⊥平面ABCD，EF∥AB，EG∥AD，EF=EG=1，AE=3