题目内容

5．某几何体的三视图如图所示，则其体积为（　　）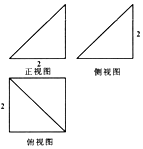
A．4B．8C．$\frac{4}{3}$D．$\frac{8}{3}$

分析 通过三视图复原的几何体是四棱锥，结合三视图的数据，求出几何体的体积．

解答 解：由题意三视图可知，几何体是四棱锥，底面边长为2的正方形，一条侧棱垂直正方形的一个顶点，长度为2，
所以几何体的体积是：$\frac{1}{3}×2×2×2$=$\frac{8}{3}$．
故选D．

点评 本题是基础题，考查三视图复原几何体的体积的求法，考查计算能力，空间想象能力．

练习册系列答案
相关题目
15．已知两定点A（-2，0），B（1，0），如果动点P满足|PA|=$\sqrt{3}$|PB|，则点P的轨迹所包围的图形的面积等于$\frac{27π}{4}$．
16．在建立两个变量y与x的回归模型中，分别选择了四个不同的模型，它们的相关指数如下，其中拟合效果最好的模型是（　　）
A．模型1的相关指数R2为0.98B．模型2的相关指数R2为0.80
C．模型3的相关指数R2为0.54D．模型4的相关指数R2为0.35
13．在梯形ABCD中，$\overrightarrow{AB}$=3$\overrightarrow{DC}$，则$\overrightarrow{BC}$等于（　　）
A．-$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AD}$B．-$\frac{2}{3}$$\overrightarrow{AB}$+$\frac{4}{3}$$\overrightarrow{AD}$C．$\frac{2}{3}$$\overrightarrow{AB}$+$\overrightarrow{AD}$D．-$\frac{2}{3}$$\overrightarrow{AB}$+$\overrightarrow{AD}$
20．已知数列{an}的前n项和为Sn，且Sn=2an-n．
（Ⅰ）证明数列{an+1}是等比数列，求数列{an}的通项公式；
（Ⅱ）记bn=$\frac{1}{{a}_{n+1}}$+$\frac{1}{{a}_{n}{a}_{n+1}}$，求数列{bn}的前n项和Tn．
10．已知函数$f（x）=lnx-\frac{1}{2}a{x^2}-2x$
（1）若函数f（x）在定义域内单调递增，求a的取值范围；
（2）若$a=-\frac{1}{2}$，且关于x的方程$f（x）=-\frac{1}{2}x+b$在[1，4]恰有两个不相等的实数根，求b的取值范围．
17．集成电路E由3个不同的电子元件组成，现由于元件老化，3个电子元件能正常工作的概率分别降为$\frac{1}{2}$，$\frac{1}{2}$，$\frac{2}{3}$，且每个电子元件能否正常工作相互独立．若3个电子元件中至少有2个正常工作，则E能正常工作，否则就需要维修，且维修集成电路E所需要费用为100元．
（1）求集成电路E需要维修的概率；
（2）若某电子设备共由2个集成电路E组成，设X为该电子设备需要维修集成电路所需费用．求X的分布列和均值．
14．已知点A（-1，2），B（2，3），若直线l：kx-y-k+1=0与线段AB相交，则实数k的取值范围是（　　）
A．（-∞，-$\frac{1}{2}$]∪[2，+∞）B．[{-$\frac{1}{2}$，2}]C．[-2，$\frac{1}{2}$]D．（-∞，-2]∪[$\frac{1}{2}$，+∞）
15．已知函数f（x）=x3-3ax+e，g（x）=1-lnx，其中e为自然对数的底数．
（Ⅰ）若曲线y=f（x）在点（1，f（1））处的切线与直线l：x+2y=0垂直，求实数a的值；
（Ⅱ）设函数$F（x）=-x[g（x）+\frac{1}{2}x-2]$，若F（x）在区间（m，m+1）（m∈Z）内存在唯一的极值点，求m的值；
（Ⅲ）用max{m，n}表示m，n中的较大者，记函数h（x）=max{f（x），g（x）}（x＞0）．若函数h（x）在（0，+∞）上恰有2个零点，求实数a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网