题目内容
20．已知$cosθ=-\frac{3}{5}$，$tanθ=\frac{4}{3}$，则角θ的终边落在（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
分析 分别由$cosθ=-\frac{3}{5}$＜0，$tanθ=\frac{4}{3}$＞0写出角θ的范围，取交集得答案．
解答 解：∵$cosθ=-\frac{3}{5}$＜0，∴θ的终边在第二、第三象限或x轴负半轴上；
∵$tanθ=\frac{4}{3}$＞0，∴θ的终边在第一、第三象限．
取交集得，角θ的终边落在第三象限．
故选：C．
点评 本题考查象限角及轴线角，考查交集思想的应用，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
8．四面体PABC的四个顶点都在球O的球面上，PA=8，BC=4，PB=PC=AB=AC，且平面PBC⊥平面ABC，则球O的表面积为（ ）
| A． | 64π | B． | 65π | C． | 66π | D． | 128π |
3．与角$-\frac{π}{3}$终边相同的角是（ ）
| A． | $\frac{5π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{11π}{6}$ | D． | $\frac{5π}{3}$ |
10．已知$\overrightarrow a=（-3，4），\overrightarrow b=（-2，1）$，则$\overrightarrow a$在$\overrightarrow b$上的投影为（ ）
| A． | -2 | B． | 2 | C． | $-2\sqrt{5}$ | D． | $2\sqrt{5}$ |
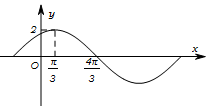已知函数f（x）=Asin（ωx+φ）．（$A＞0，ω＞0，0＜φ＜\frac{π}{2}$）的部分图象如图所示．
，∠C=
，则∠A=_______．