题目内容

15．设数列{an}是等差数列，Sn为其前n项和．若S6=8S3，a3-a5=8，则a8=-26．

分析 利用等差数列的前n项和公式和通项公式，列出方程组，求出首项和公差，由此能求出a8．

解答 解：∵数列{an}是等差数列，Sn为其前n项和．
S6=8S3，a3-a5=8，
∴$\left\{\begin{array}{l}{6{a}_{1}+\frac{6×5}{2}d=8×（3{a}_{1}+\frac{3×2}{2}d）}\\{{a}_{1}+2d-（{a}_{1}+4d）=8}\end{array}\right.$，
解得a1=2，d=-4，
∴a8=2+7×（-4）=-26．
故答案为：-26．

点评 本题考查等差数列的第8项的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．

练习册系列答案
相关题目
6．已知x、y满足约束条件$\left\{\begin{array}{l}{x-2y+7≥0}\\{4x-3y-12≤0}\\{x+2y-3≥0}\end{array}\right.$，则Z=x2+y2+2x+1的最小值是（　　）
A．$\frac{{2\sqrt{5}}}{5}$B．$\frac{16}{5}$C．2$\sqrt{41}$D．164
7．若函数f（x）=ax3-bx+4，当x=2时，函数f（x）有极值-$\frac{4}{3}$．
（1）求函数f（x）的解析式；         
（2）求函数f（x）的单调区间．
3．已知函数f（x）=x（x+1）（x+2）…（x+100），则f'（0）=100!．
10．已知函数f（x）=-$\frac{1}{2}a{x^2}+（{1+a}）x-lnx（{a∈R}）$．
（1）当a＞0时，求函数f（x）的单调减区间；
（2）当a=0时，设函数g（x）=xf（x）若存在区间$[{m，n}]?[{\frac{1}{2}，+∞}）$，使得函数g（x）在[m，n]上的值域为[k（m+2）-2，k（n+2）-2]，求实数k的取值范围．
20．已知$cosθ=-\frac{3}{5}$，$tanθ=\frac{4}{3}$，则角θ的终边落在（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
5．（1）化简f（α）=$\frac{{sin（\frac{π}{2}+α）+sin（-π-α）}}{{3cos（2π-α）+cos（\frac{3π}{2}-α）}}$； 
（2）若tanα=1，求f（α）的值．
2．下列命题：
①命题“若x2-3x+2=0，则x=1”的逆否命题为：“若x≠1，则x2-3x+2≠0”
②“x=1”是“x2-3x+2=0”的充分不必要条件
③若p∧q为假命题，则p，q均为假命题
④对于命题p：?x∈R，使得x2+x+1＜0，则￢p：?x∈R，均有x2+x+1≥0，
说法错误的是③．
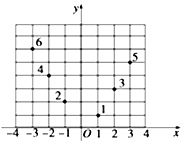2．如图所示，坐标纸上的每个单元格的边长为1，由下往上的六个点：1，2，3，4，5，6的横、纵坐标分别对应数列$\{{a_n}\}（n∈{N^*}）$的前12项，其中横坐标为奇数项，纵坐标为偶数项，按如此规律下去，则a2017+a2018+a2019等于（　　）
A．1002B．1004C．1007D．1009

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网