题目内容
8.四面体PABC的四个顶点都在球O的球面上,PA=8,BC=4,PB=PC=AB=AC,且平面PBC⊥平面ABC,则球O的表面积为( )| A. | 64π | B. | 65π | C. | 66π | D. | 128π |
分析 求出△ABC外接圆的半径,利用勾股定理求出球的半径,即可求出球O的表面积.
解答 解:由于PB=PC,取BC的中点为O',则PO'⊥BC,
由于平面ABC⊥平面PBC,
即有PO'⊥平面ABC,
∵PA=8,BC=4,PB=PC=AB=AC,
∴PB=6,PO'=4$\sqrt{2}$,
△ABC中,AB=AC=6,BC=4,
∴sin∠ABC=$\frac{4\sqrt{2}}{6}$=$\frac{2\sqrt{2}}{3}$,
∴2r=$\frac{6}{\frac{2\sqrt{2}}{3}}$,
设球的半径为R,球心到平面ABC的距离为h,
则($\frac{9}{2\sqrt{2}}$)2+h2=(4$\sqrt{2}$-h)2+(4$\sqrt{2}$-$\frac{9}{2\sqrt{2}}$)2=R2,
解得R=$\frac{\sqrt{65}}{2}$.
球O的表面积为4πR2=65π,
故选:B.
点评 本题考查面面垂直的性质定理和球的截面的性质的运用,熟记这些定理是解题的关键.

练习册系列答案
相关题目
20.设an=$\frac{1}{n}$+$\frac{1}{n+1}$+$\frac{1}{n+2}$+$\frac{1}{n+3}$+…+$\frac{1}{{n}^{2}}$(n∈N*),则a2=( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{2}$+$\frac{1}{3}$ | C. | $\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$ | D. | $\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$ |
20.已知$cosθ=-\frac{3}{5}$,$tanθ=\frac{4}{3}$,则角θ的终边落在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15.现有1名女教师和2名男教师参加说题比赛,共有2道备选题目,若每位选手从中有放回地随机选出一道题进行说题,其中恰有一男一女抽到同一道题的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
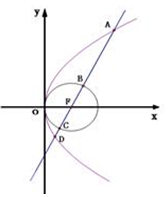 圆F:(x-1)2-y2=1和抛物线y2=4x,过F的直线l与抛物线和圆依次交于A、B、C、D四点
圆F:(x-1)2-y2=1和抛物线y2=4x,过F的直线l与抛物线和圆依次交于A、B、C、D四点