题目内容
11.已知函数y=$\left\{\begin{array}{l}(4-\frac{a}{2})x+2\;(x≤1)\\{a^x}\;\;\;(x>1)\end{array}$是R上的增函数,则实数a的取值范围是[4,8).分析 根据题意,由函数单调性的性质分析可得$\left\{\begin{array}{l}{4-\frac{a}{2}>0}\\{a>1}\\{(4-\frac{a}{2})+2≤a}\end{array}\right.$,解可得a的取值范围,即可得答案.
解答 解:根据题意,函数y=$\left\{\begin{array}{l}(4-\frac{a}{2})x+2\;(x≤1)\\{a^x}\;\;\;(x>1)\end{array}$是R上的增函数,
则有$\left\{\begin{array}{l}{4-\frac{a}{2}>0}\\{a>1}\\{(4-\frac{a}{2})+2≤a}\end{array}\right.$,
解可得4≤a<8,
即a的取值范围是[4,8);
故答案为:[4,8).
点评 本题考查函数单调性的性质及应用,关键是掌握函数单调性的图象特点.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
20.设an=$\frac{1}{n}$+$\frac{1}{n+1}$+$\frac{1}{n+2}$+$\frac{1}{n+3}$+…+$\frac{1}{{n}^{2}}$(n∈N*),则a2=( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{2}$+$\frac{1}{3}$ | C. | $\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$ | D. | $\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$ |
20.已知$cosθ=-\frac{3}{5}$,$tanθ=\frac{4}{3}$,则角θ的终边落在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
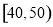 ,
,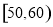 ,…,
,…,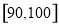 后得到如下频率分布直方图.
后得到如下频率分布直方图.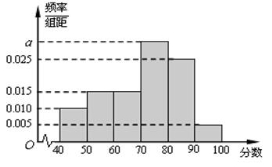
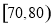 内的频率;
内的频率;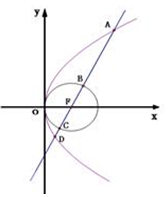 圆F:(x-1)2-y2=1和抛物线y2=4x,过F的直线l与抛物线和圆依次交于A、B、C、D四点
圆F:(x-1)2-y2=1和抛物线y2=4x,过F的直线l与抛物线和圆依次交于A、B、C、D四点