题目内容

解关于x的不等式ax2-2x＞ax-2．
考点：指、对数不等式的解法
专题：不等式的解法及应用
分析：分a＞1和0＜a＜1两种情况，分别利用指数函数的单调性求得不等式的解集．
解答： 解：（1）a＞1时，由不等式可得 x2-2x＞x-2，求得x＜1，或x＞2，
故不等式的解集为{x|x＜1，或x＞2}．
（2）当0＜a＜1时，由不等式可得 x2-2x＜x-2，求得1＜x＜2，故不等式的解集为{x|1＜x＜2}．
点评：本题主要考查指数不等式的解法，体现了转化、分类讨论的数学思想，属于基础题．
练习册系列答案
相关题目
若角α的终边经过点P（-1，2），则sinα等于（　　）
A、-
5
5
B、
2
5
5
C、
5
5
D、-
2
5
5
写出下列命题的否定：
（1）所有自然数的平方是正数；
（2）任何实数x都是方程5x-12=0的根；      
（3）对于任意实数x，存在实数y，使x+y＞0；
（4）有些质数是奇数．
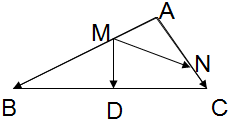如图：在△ABC中，D为BC中点，AM=
1
3
AB，AN=
2
3
AC，设
AB
=
a
，
AC
AC
=
b
．
（Ⅰ）试用
a
，
b
表示
MN
；       
（Ⅱ）试用
a
，
b
表示
MD
．
已知函数f（x）=kx+b（k≠0，1）．
（1）求f（f（f（x）））；
（2）求f（f（f（…f（x）））．
函数f（x）=exsinx在区间[0，
π
2
]上的值域．
已知定义在区间（0，+∞）上的函数f（x）满足f（
x1
x2
）=f（x1）-f（x2），且当x＞1时，f（x）＜0．
（1）求f（1）的值；
（2）判断函数f（x）的单调性．
设函数f（x）是定义在区间（-∞，+∞）上的偶函数，且满足f（1-x）=f（1+x）（x∈R）．
（1）求函数f（x）的周期；
（2）已知当x∈（-1，1]时，f（x）=1-
1-x2
，求使方程f（x）=ax在x∈（-1，1]上有两个不相等实根a的取值集合M；
（3）记Ik=（2k-1，2k+1]（k∈N，k≥1），Mk表示使方程f（x）=ax在x∈Ik上有两个不相等实根的a的取值集合，求集合Mk．
在集合{（x，y），0≤x≤5，且0≤y≤4}内任取一个元素，能使代数式
y
3
+
x
4
-
19
12
≥0的概率是多少？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网