题目内容
已知函数f（x）=kx+b（k≠0，1）．
（1）求f（f（f（x）））；
（2）求f（f（f（…f（x）））．
（1）求f（f（f（x）））；
（2）求f（f（f（…f（x）））．
考点：函数的值
专题：函数的性质及应用
分析：利用函数的性质求解．
解答：
解：（1）∵f（x）=kx+b，
∴f（f（x））=f（kx+b）=k2x+kb+b，
f（f（f（x）））=f（k2x+kb+b）=k3x+k2b+kb+b．
（2）由（1）知f（f（f（…f（x）））
=knx+kn-1b+kn-2b+…+kb+b．
∴f（f（x））=f（kx+b）=k2x+kb+b，
f（f（f（x）））=f（k2x+kb+b）=k3x+k2b+kb+b．
（2）由（1）知f（f（f（…f（x）））
=knx+kn-1b+kn-2b+…+kb+b．
点评：本题考查函数值的求法，是基础题，解题时要注意函数性质的合理运用．
练习册系列答案
相关题目
在三角形ABC中，如果a2+c2-b2=ac，那么B等于（ ）
| A、30° | B、60° |
| C、120° | D、150° |
设集合M={x|x≤
}，N={1，2，3，4}，则M∩N的运算结果为（ ）
| 2 |
| A、{1} |
| B、{3，4} |
| C、{2，3，4} |
| D、{1，2，3，4} |
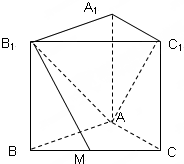如图，正三棱柱ABC-A1B1C1中，点M是BC的中点，AB=2，BB1=