题目内容
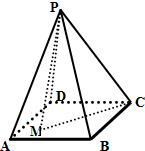如图，在四棱锥P-ABCD中，侧面PAD为正三角形，底面为正方形，侧面PAD与底面ABCD垂直，M为底面所在平面内的一个动点，若动点M到点C的距离等于点M到面PAD的距离，则动点M的轨迹为（ ）| A、椭圆 | B、抛物线 |
| C、双曲线 | D、直线 |
考点：平面与平面垂直的性质
专题：空间位置关系与距离
分析：根据面面垂直的性质推断出即点M到直线AD的距离，即为点M到平面PAD的距离，进而根据抛物线的定义推断出点M的轨迹为抛物线．
解答：
解：∵侧面PAD与底面ABCD垂直，且AD为二面的交线，
∴点M向AD作垂线，垂线一定垂直于平面PAD，
即点M到直线AD的距离，即为点M到平面PAD的距离，
∴动点M到点C的距离等于点M直线的距离，
根据抛物线的定义可知，M点的轨迹为抛物线．
故选B．
∴点M向AD作垂线，垂线一定垂直于平面PAD，
即点M到直线AD的距离，即为点M到平面PAD的距离，
∴动点M到点C的距离等于点M直线的距离，
根据抛物线的定义可知，M点的轨迹为抛物线．
故选B．
点评：本题主要考查了平面与平面垂直的性质．在平面与平面垂直的问题上，要特别注意两面的交线．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
已知向量
=（1，0），
=（0，-1），
=k2
+k
（k≠0），
=
+
，如果
∥
，那么（ ）
| a |
| b |
| c |
| a |
| b |
| d |
| a |
| b |
| c |
| d |
A、k=1且
| ||||
B、k=1且
| ||||
C、k=-1且
| ||||
D、k=-1且
|
在区间[0，2]内随机取一个数a，则使得函数f（x）=
x3-
ax2-2a2x+
有三个零点的概率为（ ）
| 1 |
| 3 |
| 1 |
| 2 |
| 10 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
| D、1 |
已知sinθ=
，且cosθ＜0，则tanθ等于（ ）
| 3 |
| 5 |
A、-
| ||
B、
| ||
| C、-3 | ||
| D、3 |
在复平面内，复数i（i+1）的虚部为（ ）
| A、-1 | B、1 |
| C、i | D、i2 |
化简log2
+log25等于（ ）
| 4 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
| D、2 |