题目内容

已知sinθ=
3
5
，且cosθ＜0，则tanθ等于（　　）
A、-
3
4
B、
3
4
C、-3
D、3
考点：同角三角函数间的基本关系
专题：三角函数的求值
分析：根据cosθ的值小于0，由sinθ的值，利用同角三角函数间的基本关系求出cosθ的值，即可确定出tanθ的值．
解答： 解：∵sinθ=
3
5
，且cosθ＜0，
∴cosθ=-
1-sin2θ
=-
4
5
，
则tanθ=
sinθ
cosθ
=-
3
4
．
故选：A．
点评：此题考查了同角三角函数间的基本关系，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
若从不包括大小王的52张扑克牌中随机抽取一张，取到红心的概率是
1
4
，取到方片的概率是
1
4
，则取到红色牌的概率为（　　）
A、
1
4
B、
1
3
C、
1
2
D、
3
4
对实数m、n，定义运算“*”：m*n=
m(m-n≤1)
n(m-n＞1)
，设函数f（x）=（x2-3）*（x-2），x∈R．若函数y=f（x）+c的图象与x轴恰有两个公共点，则实数c的取值范围是（　　）
A、（-3，1）
B、（-3，1]
C、（-3，-2]∪（0，1]
D、[2，3）∪[-1，0）
已知过双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的右焦点且倾斜角为45°的直线与双曲线的右支有两个交点，则双曲线的离心率e的取值范围是（　　）
A、（1，
3
）
B、（1，
3
]
C、（1，
2
]
D、（1，
2
）
已知在△ABC中，角A，B，C的对边分别为a，b，c，已知点D是边BC的中点，且2
AD
•
BC
=a2-ac，则B的大小为（　　）
A、45°B、60°
C、90°D、120°
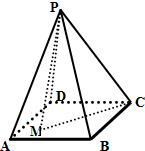如图，在四棱锥P-ABCD中，侧面PAD为正三角形，底面为正方形，侧面PAD与底面ABCD垂直，M为底面所在平面内的一个动点，若动点M到点C的距离等于点M到面PAD的距离，则动点M的轨迹为（　　）
A、椭圆B、抛物线
C、双曲线D、直线
一名老师和两名男生两名女生站成一排照相，要求两名女生必须站在一起且老师不站在两端，则不同站法的种数为（　　）
A、8B、12C、16D、24
某大型企业人力资源部为了研究企业员工工作积极性和对待企业改革态度的关系，随机抽取了180名员工进行调查，在被调查员工中有100名工作积极，80名工作一般，120名积极支持企业改革，60名不太赞成企业改革，工作积极的员工里有80%积极支持企业改革．
（1）作出2×2列联表
积极支持企业改革 不太赞成企业改革 合计
工作积极
工作一般
合计
（2）对于人力资源部的研究项目进行分析，根据上述数据能否有99.9%的把握认为工作积极性与对待企业改革态度有关？
附：K2=
n(ad-bc)2
(a+b)(c+d)(a+c)(b+d)

P（K2≥K0） 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
K0 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
已知集合A={x|x2+2x＜0}，B={x|y=
x+1
}
（1）求A∪B，（∁RA）∩B
（2）若集合C={x|2a＜x＜a+1}且C⊆A，求a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网