题目内容
已知△ABC中,∠ACB=90°,AB=2BC=2,将△ABC绕BC旋转得△PBC,当直线PC与平面PAB所成角的正弦值为
时,P、A两点间的距离是( )
| ||
| 6 |
| A、2 | ||
| B、4 | ||
C、2
| ||
D、2
|
考点:直线与平面所成的角,两点间的距离公式,点、线、面间的距离计算
专题:综合题,空间角
分析:过C作CE⊥BD,E为垂足,由题意得到∠CPE就是直线PC与平面PAB所成角,利用直线PC与平面PAB所成角的正弦值为
,PC=
,求出CE,再求出CD,可得PD,即可得出结论.
| ||
| 6 |
| 3 |
解答:
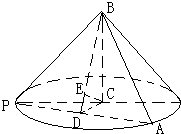 解:过C作CE⊥BD,E为垂足,由于PA⊥平面BCD,
解:过C作CE⊥BD,E为垂足,由于PA⊥平面BCD,
∴平面BCD⊥平面PBA,由两个平面互相垂直的性质可知:CE⊥平面PBA,
∴∠CPE就是直线PC与平面PAB所成角,
∵直线PC与平面PAB所成角的正弦值为
,PC=
,
∴CE=
,
设CD=x,则BD=
,
∴
•1•x=
•
•
,
∴x=1,
∵PC=
,
∴PD=
,
∴PA=2PD=2
.
故选:C.
 解:过C作CE⊥BD,E为垂足,由于PA⊥平面BCD,
解:过C作CE⊥BD,E为垂足,由于PA⊥平面BCD,∴平面BCD⊥平面PBA,由两个平面互相垂直的性质可知:CE⊥平面PBA,
∴∠CPE就是直线PC与平面PAB所成角,
∵直线PC与平面PAB所成角的正弦值为
| ||
| 6 |
| 3 |
∴CE=
| ||
| 2 |
设CD=x,则BD=
| 1+x2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1+x2 |
| ||
| 2 |
∴x=1,
∵PC=
| 3 |
∴PD=
| 2 |
∴PA=2PD=2
| 2 |
故选:C.
点评:本题考查直线与平面所成角的正弦值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
若
=(cosα,sinα),
=(cosβ,sinβ),则( )
| a |
| b |
A、
| ||||||||
B、
| ||||||||
C、(
| ||||||||
D、(
|
若从不包括大小王的52张扑克牌中随机抽取一张,取到红心的概率是
,取到方片的概率是
,则取到红色牌的概率为( )
| 1 |
| 4 |
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知向量
=(2,3),
=(3,-2),则
•
=( )
| a |
| b |
| a |
| b |
| A、2 | B、-2 | C、1 | D、0 |
对任意正数x,y不等式(k-
)x+ky≥
恒成立,则实数k的最小值是( )
| 1 |
| 2 |
| 2xy |
| A、1 | B、2 | C、3 | D、4 |
已知数列{an}满足a1=1,an+1=an+n,则a3的值为( )
| A、2 | B、3 | C、4 | D、5 |
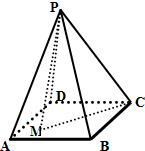 如图,在四棱锥P-ABCD中,侧面PAD为正三角形,底面为正方形,侧面PAD与底面ABCD垂直,M为底面所在平面内的一个动点,若动点M到点C的距离等于点M到面PAD的距离,则动点M的轨迹为( )
如图,在四棱锥P-ABCD中,侧面PAD为正三角形,底面为正方形,侧面PAD与底面ABCD垂直,M为底面所在平面内的一个动点,若动点M到点C的距离等于点M到面PAD的距离,则动点M的轨迹为( )