题目内容

化简log2
4
5
+log25等于（　　）
A、
29
10
B、
10
29
C、
1
2
D、2
考点：对数的运算性质
专题：函数的性质及应用
分析：利用对数运算法则求解．
解答： 解：log2
4
5
+log25
=log2(
4
5
×5)
=log24
=2．
故选：D．
点评：本题考查对数的化简求值，是基础题，解题时要注意对数的运算性质和运算法则的合理运用．
练习册系列答案
相关题目
对任意正数x，y不等式（k-
1
2
）x+ky≥
2xy
恒成立，则实数k的最小值是（　　）
A、1B、2C、3D、4
已知过双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的右焦点且倾斜角为45°的直线与双曲线的右支有两个交点，则双曲线的离心率e的取值范围是（　　）
A、（1，
3
）
B、（1，
3
]
C、（1，
2
]
D、（1，
2
）
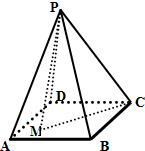如图，在四棱锥P-ABCD中，侧面PAD为正三角形，底面为正方形，侧面PAD与底面ABCD垂直，M为底面所在平面内的一个动点，若动点M到点C的距离等于点M到面PAD的距离，则动点M的轨迹为（　　）
A、椭圆B、抛物线
C、双曲线D、直线
一名老师和两名男生两名女生站成一排照相，要求两名女生必须站在一起且老师不站在两端，则不同站法的种数为（　　）
A、8B、12C、16D、24
已知函数f（x）=mx+n，当x∈[a1，b1]时，值域为[a2，b2]，当x∈[a2，b2]时，值域为[a3，b3]，…，当x∈[an-1，bn-1]时，值域为[an，bn]，其中m，n为常数，a1=0，b1=1
（1）若m=-1，n=0，求an；
（2）若m=3，设数列{an}与{bn]的前n项和分别为Sn和Tn，求T2014-S2014；
（3）若m=2，n=1，求证：
n
2
-
1
3
＜
b1
b2
+
b2
b3
+…+
bn
n+1b 
＜
n
2
．
某大型企业人力资源部为了研究企业员工工作积极性和对待企业改革态度的关系，随机抽取了180名员工进行调查，在被调查员工中有100名工作积极，80名工作一般，120名积极支持企业改革，60名不太赞成企业改革，工作积极的员工里有80%积极支持企业改革．
（1）作出2×2列联表
积极支持企业改革 不太赞成企业改革 合计
工作积极
工作一般
合计
（2）对于人力资源部的研究项目进行分析，根据上述数据能否有99.9%的把握认为工作积极性与对待企业改革态度有关？
附：K2=
n(ad-bc)2
(a+b)(c+d)(a+c)(b+d)

P（K2≥K0） 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
K0 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
袋子中装有除颜色外其他均相同的编号为a，b的2个黑球和编号为c，d，e的3个红球，从中任意摸出2个球．
（1）写出所有不同的结果；
（2）求恰好摸出1个黑球和1个红球的概率．
已知5个乒乓球，其中3个新的，2个旧的，每次取1个，不放回的取两次，求：
（1）第一次取到新球的概率．
（2）第二次取到新球的概率．
（3）在第一次取到新球的条件下第二次取到新球的概率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网