题目内容
已知向量
=(1,0),
=(0,-1),
=k2
+k
(k≠0),
=
+
,如果
∥
,那么( )
| a |
| b |
| c |
| a |
| b |
| d |
| a |
| b |
| c |
| d |
A、k=1且
| ||||
B、k=1且
| ||||
C、k=-1且
| ||||
D、k=-1且
|
考点:平行向量与共线向量
专题:平面向量及应用
分析:利用已知条件求出
,
,通过
∥
,求出k的值,判断选项即可.
| c |
| d |
| c |
| d |
解答:
解:向量
=(1,0),
=(0,-1),
=k2
+k
=(k2,-k),
=
+
=(1,-1),
∵
∥
,
∴-k2=-k,解得k=1或k=0(舍去),
此时
=(1,-1),
=(1,-1),两个向量相同.
故选:A.
| a |
| b |
| c |
| a |
| b |
| d |
| a |
| b |
∵
| c |
| d |
∴-k2=-k,解得k=1或k=0(舍去),
此时
| c |
| d |
故选:A.
点评:本题考查向量的共线以及向量的坐标运算,基本知识的考查.

练习册系列答案
相关题目
对任意正数x,y不等式(k-
)x+ky≥
恒成立,则实数k的最小值是( )
| 1 |
| 2 |
| 2xy |
| A、1 | B、2 | C、3 | D、4 |
已知数列{an}满足a1=1,an+1=an+n,则a3的值为( )
| A、2 | B、3 | C、4 | D、5 |
对实数m、n,定义运算“*”:m*n=
,设函数f(x)=(x2-3)*(x-2),x∈R.若函数y=f(x)+c的图象与x轴恰有两个公共点,则实数c的取值范围是( )
|
| A、(-3,1) |
| B、(-3,1] |
| C、(-3,-2]∪(0,1] |
| D、[2,3)∪[-1,0) |
从1,2,3,4,5中任取3个数字组成没有重复数字的三位数,共有个数是( )
| A、10 | B、20 | C、30 | D、60 |
已知过双曲线C:
-
=1(a>0,b>0)的右焦点且倾斜角为45°的直线与双曲线的右支有两个交点,则双曲线的离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(1,
| ||
B、(1,
| ||
C、(1,
| ||
D、(1,
|
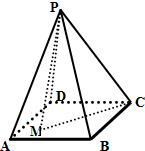 如图,在四棱锥P-ABCD中,侧面PAD为正三角形,底面为正方形,侧面PAD与底面ABCD垂直,M为底面所在平面内的一个动点,若动点M到点C的距离等于点M到面PAD的距离,则动点M的轨迹为( )
如图,在四棱锥P-ABCD中,侧面PAD为正三角形,底面为正方形,侧面PAD与底面ABCD垂直,M为底面所在平面内的一个动点,若动点M到点C的距离等于点M到面PAD的距离,则动点M的轨迹为( )