题目内容
5.已知椭圆$\frac{x^2}{4}+\frac{y^2}{3}$=1的左顶点为A,右焦点为F2,点P是椭圆上一动点,则当$\overrightarrow{P{F_2}}•\overrightarrow{PA}$取最小值时,$|{\overrightarrow{PA}+\overrightarrow{P{F_2}}}$|=3.分析 由椭圆的方程求得左顶点为A(-2,0)右焦点为F2(1,0),由y2=3-$\frac{3}{4}$x2,根据向量的坐标得出$\overrightarrow{PA}$•$\overrightarrow{P{F}_{2}}$=(-2-x,-y)•(1-x,-y)=$\frac{1}{4}$(x+2)2,-2≤x≤2,利用函数性质,求出P点坐标,即可得出答案.
解答 解:由椭圆$\frac{x^2}{4}+\frac{y^2}{3}$=1的左顶点为A,右焦点为F2,P(x,y)
∴左顶点为A(-2,0)右焦点为F2(1,0),
$\overrightarrow{PA}$=(-2-x,-y),$\overrightarrow{P{F}_{2}}$=(1-x,-y)
∴$\overrightarrow{PA}$•$\overrightarrow{P{F}_{2}}$=(-2-x,-y)•(1-x,-y)=(1-x)(-2-x)+y2,
∵点P为椭圆上一动点,
y2=3-$\frac{3}{4}$x2,代入得:$\overrightarrow{PA}$•$\overrightarrow{P{F}_{2}}$=$\frac{1}{4}$(x+2)2,-2≤x≤2,
∴当x=-2时,$\overrightarrow{PA}$•$\overrightarrow{P{F}_{2}}$最小,y2=3-$\frac{3}{4}$×4=0,
∴P(-2,0)时$\overrightarrow{PA}$=(0,0),$\overrightarrow{P{F}_{2}}$=(3,0)
丨$\overrightarrow{PA}$•$\overrightarrow{P{F}_{2}}$丨的值为3,
故答案为:3.
点评 本题考查椭圆的标准方程及性质,考查向量数量积的坐标运算,考查一元二次函数的性质,考查计算能力,属于中档题.

 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案| A. | m⊥l,m∥n,则n∥l | B. | 若m∥α,n∥α,则m∥n | C. | 若m⊥α,n?α,则m⊥n | D. | 若m∥α,n?α,则m∥n |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
| A. | a<1 | B. | a≤1 | C. | a<2 | D. | a≤2 |
| A. | $\frac{1}{2}$ | B. | -1 | C. | 2 | D. | 1 |
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
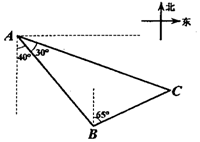 如图所示,一艘海轮从A处出发,以每小时40海里的速度沿南偏东40°方向直线航行,30分钟后到达B处,在C处有一座灯塔,海轮在A处观察灯塔,其方向是南偏东70°,在B处观察灯塔,其方向是北偏东65°,那么B、C两点间的距离是10$\sqrt{2}$海里.
如图所示,一艘海轮从A处出发,以每小时40海里的速度沿南偏东40°方向直线航行,30分钟后到达B处,在C处有一座灯塔,海轮在A处观察灯塔,其方向是南偏东70°,在B处观察灯塔,其方向是北偏东65°,那么B、C两点间的距离是10$\sqrt{2}$海里.