已知p:＞0,q:|x|＜a.若￢p是q的必要不充分条件.则a的取值范围是( )A．a＜1B．a≤1C．a＜2D．a≤2 题目和参考答案——青夏教育精英家教网—

题目内容

10．已知p：（x-2）（x+1）＞0；q：|x|＜a，若￢p是q的必要不充分条件，则a的取值范围是（　　）

A．

a＜1

B．

a≤1

C．

a＜2

D．

a≤2

分析分别求出关于p，q成立的x的范围，根据集合的包含关系判断即可．

解答解：由（x-2）（x+1）＞0；解得：x＞2或x＜-1，
故p：x＞2或x＜-1；
由|x|＜a，a＞0时解得：-a＜x＜a，
a≤0时，无解
若￢p是q的必要不充分条件，
即q是￢p的充分不必要条件，
a≤0时，显然成立，
a＞0时，即（-a，a）⊆[-1，2]，
故a≤1，
故选：B．

点评本题考查了充分必要条件，考查集合的包含关系以及解不等式问题，是一道基础题．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

19．已知向量$\overrightarrow{a}$=（1，1），$\overrightarrow{b}$=（m，2），且$\overrightarrow{a}$•$\overrightarrow{b}$=1，则m的值为-1，a与b夹角的余弦值等于$\frac{\sqrt{10}}{10}$．

16．已知函数f（x）=x³+x²-x+1，则此函数在[-2，$\frac{1}{2}$]上的最大值等于2．

5．已知椭圆$\frac{x^2}{4}+\frac{y^2}{3}$=1的左顶点为A，右焦点为F₂，点P是椭圆上一动点，则当$\overrightarrow{P{F_2}}•\overrightarrow{PA}$取最小值时，$|{\overrightarrow{PA}+\overrightarrow{P{F_2}}}$|=3．

15．△ABC满足下列条件：①b=12，c=9，C=60°②b=3，c=4，B=30°；③b=3$\sqrt{3}$，c=6，B=60°；④a=5，b=8，A=30°．其中有两个解的是（　　）

2．

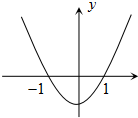设f（x）=ax³+bx²+cx的极小值为-2，其导函数y=f′（x）的图象是经过点（-1，0），（1，0）开口向上的抛物线，如图所示．
（1）求f（x）的解析式；
（2）若m≠-2，且过点（1，m）可作曲线y=f（x）的三条切线，求实数m的取值范围．

19．若a=log${\;}_{\frac{1}{2}}}$3，b=log₃$\frac{1}{2}$，c=2^0.3，则（　　）

20．化简求值：
（1）$2\sqrt{3}×\root{3}{1.5}×\root{6}{12}×\sqrt{{{（3-π）}^2}}$；
（2）$lg25+\frac{2}{3}lg8+lg5•lg20+{（lg2）^2}$．

试题分类