题目内容
18．
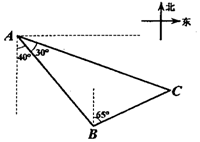如图所示，一艘海轮从A处出发，以每小时40海里的速度沿南偏东40°方向直线航行，30分钟后到达B处，在C处有一座灯塔，海轮在A处观察灯塔，其方向是南偏东70°，在B处观察灯塔，其方向是北偏东65°，那么B、C两点间的距离是10$\sqrt{2}$海里．
分析 根据题意，确定∠BAC、∠ABC的值，进而可得到∠ACB的值，根据正弦定理可得到BC的值．
解答 解：如图，由已知可得，∠BAC=30°，∠ABC=105°，AB=20，
从而∠ACB=45°．
在△ABC中，由正弦定理可得BC=$\frac{AB}{sin45°}$×sin30°=10$\sqrt{2}$海里．
故答案为10$\sqrt{2}$．
点评 本题主要考查正弦定理的应用，考查三角形的解法，属于基本知识的考查．
练习册系列答案
相关题目
8．已知关于x的不等式kx2-6kx+k+8≥0对任意x∈R恒成立，则k的取值范围是（ ）
| A． | 0≤k≤1 | B． | 0＜k≤1 | C． | k＜0或k＞1 | D． | k≤0或k≥1 |
9．将函数y=sin2x的图象向左平移$\frac{π}{3}$个单位长度，所得图象的函数解析式为（ ）
| A． | y=sin（2x+$\frac{π}{3}$） | B． | y=sin（2x-$\frac{π}{3}$） | C． | y=sin（2x+$\frac{2π}{3}$） | D． | y=sin（2x+$\frac{π}{6}$） |
6．函数y=sinx•cosx，x∈R的最小正周期为（ ）
| A． | 2 | B． | π | C． | 2π | D． | $\frac{1}{π}$ |
13．
已知正四面体ABCD中，E是AB的中点，则异面直线CE与BD所成角的余弦值为（ ）
已知正四面体ABCD中，E是AB的中点，则异面直线CE与BD所成角的余弦值为（ ）| A． | $\frac{\sqrt{3}}{6}$ | B． | $\frac{\sqrt{6}}{3}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | 0 |
《中华人民共和国道路交通安全法》规定：车辆驾驶员血液酒精浓度在20一80 mg/l00mL（不含80）之间，属于酒后驾车；血液酒精浓度在80mg/l00mL（含80）以上时，属醉酒驾车．据有关调查，在一周内，某地区查处酒后驾车和醉酒驾车共300人．如图是对这300人血液中酒精含量进行检测所得结果的频率分布直方图，则属于醉酒驾车的人数约为（ ）
10．下列函数能用二分法求零点的是（ ）
| A． | f（x）=x2 | B． | f（x）=$\sqrt{-{x^2}+1}$ | C． | f（x）=ln（x+2）2 | D． | f（x）=$\frac{1}{{|{{2^x}-3}|}}$ |