题目内容
已知直线的极坐标方程为ρcosθ-ρsinθ+2=0,则它与曲线
(α为参数)的交点的直角坐标是 .
|
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:化极坐标方程为直角坐标方程,化参数方程为普通方程,然后联立方程组求解.
解答:
解:由ρcosθ-ρsinθ+2=0,得x-y+2=0,
由
,①式两边平方得:x2=1+sin2α③,
把②代入③得:x2=y.(0≤y≤2)
联立
,解得:
或
(舍去).
∴两曲线交点的直角坐标为(-1,1).
故答案为:(-1,1).
由
|
把②代入③得:x2=y.(0≤y≤2)
联立
|
|
|
∴两曲线交点的直角坐标为(-1,1).
故答案为:(-1,1).
点评:本题考查了化曲线的极坐标方程为直角坐标方程,考查了直线与圆锥曲线的关系,是基础题.

练习册系列答案
相关题目
关于幂函数f(x)=x3,若0<x1<x2,则f(
)、
的大小关系( )
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
A、f(
| ||||
B、f(
| ||||
C、f(
| ||||
| D、无法确定 |
已知f(cosx)=cos17x,则f(sinx)的结果是( )
| A、sin17x | ||
| B、cos17x | ||
C、sin
| ||
D、cos
|
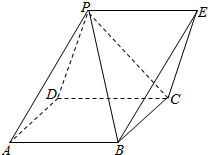 有一个所有棱长均为a的正四棱锥P-ABCD,还有一个所有棱长均为a的正三棱锥,将此三棱锥的一个面与正四棱锥的一个侧面完全重合的黏在一起,得到一个如图所示的多面体;
有一个所有棱长均为a的正四棱锥P-ABCD,还有一个所有棱长均为a的正三棱锥,将此三棱锥的一个面与正四棱锥的一个侧面完全重合的黏在一起,得到一个如图所示的多面体;